《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

8. 如图，将一副三角板按图中所示位置摆放，点$F$在$AC$上，其中$\angle ACB = 90^{\circ}$，$\angle ABC = 60^{\circ}$，$\angle EFD = 90^{\circ}$，$\angle DEF = 45^{\circ}$，$AB// DE$，则$\angle EFC$的度数是（ ）



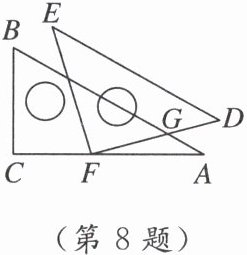
A. $60^{\circ}$
B. $65^{\circ}$
C. $70^{\circ}$
D. $75^{\circ}$

答案： D@@【点拨】因为∠EFD = 90°，所以∠DEF + ∠EDF = 90°. 因为∠DEF = 45°，所以∠EDF = 90° - ∠DEF = 90° - 45° = 45°. 因为AB//DE，所以∠BGF = ∠EDF = 45°. 因为∠ACB = 90°，所以∠ABC + ∠BAC = 90°. 因为∠ABC = 60°，所以∠BAC = 30°. 因为∠BGF + ∠AGF = 180°，∠AFG + ∠GAF + ∠AGF = 180°，所以∠BGF = ∠AFG + ∠GAF，即45° = ∠AFG + 30°. 所以∠AFG = 15°. 因为∠EFD = 90°，所以∠EFC = 180° - ∠AFG - ∠EFD = 180° - 15° - 90° = 75°.

9. [2024·聊城茌平区一模] 如图，$AB// EF$，$\angle C = 90^{\circ}$，则$\alpha$，$\beta$，$\gamma$的关系为（ ）

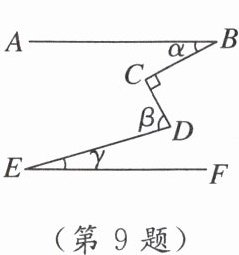
A. $\beta=\alpha+\gamma$
B. $\alpha+\beta+\gamma = 180^{\circ}$
C. $\beta+\gamma-\alpha = 90^{\circ}$
D. $\alpha+\beta-\gamma = 90^{\circ}$

答案：
D@@【点拨】如图，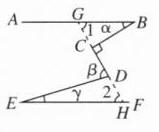
延长DC交AB与G，延长CD交EF于H. 因为∠BCD = 90°，所以∠BCG = 90°. 所以∠1 = 90° - α. 在△EHD中，∠2 = 180° - (180° - β) - γ = β - γ. 因为AB//EF，所以∠1 = ∠2，所以90° - α = β - γ，故α + β - γ = 90°.

10. [2024·泰安岱岳区模拟] 如图是路政工程车的工作示意图，工作篮底部与支撑平台平行. 若$\angle 1 = 35^{\circ}$，$\angle 3 = 155^{\circ}$，则$\angle 2$的度数为（ ）

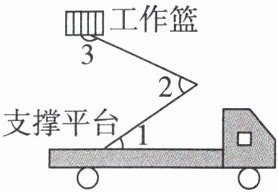
A. $50^{\circ}$
B. $60^{\circ}$
C. $65^{\circ}$
D. $55^{\circ}$

答案：
B@@【点拨】如图所示，
过∠2顶点O作直线EF//CD. 因为AB//CD，所以AB//EF//CD. 所以∠3 + ∠EON = 180°， ∠1 = ∠MOE. 因为∠3 = 155°，∠1 = 35°， 所以∠EON = 25°，∠MOE = 35°. 所以∠MON = ∠MOE + ∠EON = 60°，即∠2 = 60°.

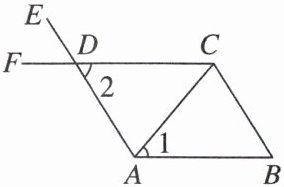
11. [2024·潍坊高密市期中] 如图，$AE// BC$，$\angle BAD=\angle BCD$.
(1)$AB$与$CD$平行吗？请说明理由.
(2)若$AC$平分$\angle BAD$，且$\angle 1+\angle 2 = 115^{\circ}$，求$\angle ADF$的度数.

答案： 【解】
(1)AB//CD，理由如下： 因为AE//BC，所以∠BAD + ∠B = 180°. 因为∠BAD = ∠BCD，所以∠BCD + ∠B = 180°，所以AB//CD.
(2)因为AB//CD，所以∠2 + ∠BAD = 180°，∠ADF = ∠BAD. 因为AC平分∠BAD，所以∠BAD = 2∠1. 所以∠2 + 2∠1 = 180°. 又因为∠1 + ∠2 = 115°，所以∠1 = 65°. 所以∠BAD = 2×65° = 130°. 所以∠ADF = ∠BAD = 130°.

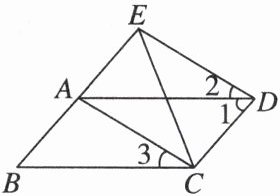
12. 如图，已知$AD// BC$，$\angle 1=\angle B$，$\angle 2=\angle 3$.
(1)请写出图中除$AD$和$BC$之外的平行直线，并说明理由.
(2)结合（1）中所得的结论，判断$\angle BED$与$\angle ACD$的数量关系，并说明理由.

答案： 【解】
(1)AB//CD，AC//DE. 理由：因为AD//BC，所以∠B + ∠BAD = 180°. 又因为∠1 = ∠B，所以∠1 + ∠BAD = 180°. 所以AB//CD. 因为AD//BC，所以∠DAC = ∠3. 又因为∠2 = ∠3，所以∠2 = ∠DAC. 所以AC//ED.
(2)∠BED = ∠ACD. 理由：因为AC//ED，所以∠BAC = ∠BED. 因为AE//CD，所以∠ACD = ∠BAC. 所以∠BED = ∠ACD.

13. [学科素养·推理能力]（1）【感知与探究】如图①，直线$AB// CD$，过点$E$作$EF// AB$. 请直接写出$\angle B$，$\angle D$，$\angle BED$之间的数量关系：____________________；
（2）【应用与拓展】如图②，直线$AB// CD$. 若$\angle B = 23^{\circ}$，$\angle G = 35^{\circ}$，$\angle D = 25^{\circ}$，借助（1）中的结论，求$\angle BEG+\angle GFD$的度数；
（3）【方法与实践】如图③，直线$AB// CD$. 若$\angle E=\angle B = 60^{\circ}$，$\angle F = 85^{\circ}$，则$\angle D =$________$^{\circ}$.

答案：
$\angle BED = \angle B + \angle D$@@25@@【解】
(2)如图，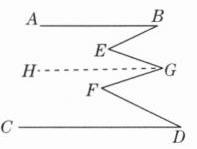
过点G作GH//AB. 又因为AB//CD，所以GH//CD//AB. 由
(1)可得∠BEG = ∠B + ∠EGH，∠GFD = ∠D + ∠FGH. 因为∠B = 23°，∠EGF = 35°，∠D = 25°， 所以∠BEG + ∠GFD = ∠B + ∠EGH + ∠D + ∠FGH = ∠B + ∠D + ∠EGF = 23° + 25° + 35° = 83°.