第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
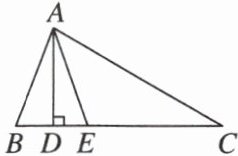
1. [2024·青岛市北区月考] 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B = 70°,∠C = 30°.
(1)∠BAE = ________;
(2)分别求出∠DAE与∠DEA的度数.
(1)∠BAE = ________;
(2)分别求出∠DAE与∠DEA的度数.

答案:
【解】
(1)$40^{\circ}$
(2)$\because\angle B = 70^{\circ},\angle C = 30^{\circ},\therefore\angle BAC = 80^{\circ}$. $\because AD\perp BC,\therefore\angle ADC = 90^{\circ}$. $\because$在直角三角形$ACD$中,$\angle DAC = 90^{\circ}-\angle C = 60^{\circ}$. $\because AE$平分$\angle BAC,\therefore\angle EAC = 40^{\circ}$. $\therefore\angle DAE=\angle DAC - \angle EAC = 20^{\circ}$. $\therefore\angle DEA = 90^{\circ}-\angle DAE = 90^{\circ}-20^{\circ}=70^{\circ}$.
(1)$40^{\circ}$
(2)$\because\angle B = 70^{\circ},\angle C = 30^{\circ},\therefore\angle BAC = 80^{\circ}$. $\because AD\perp BC,\therefore\angle ADC = 90^{\circ}$. $\because$在直角三角形$ACD$中,$\angle DAC = 90^{\circ}-\angle C = 60^{\circ}$. $\because AE$平分$\angle BAC,\therefore\angle EAC = 40^{\circ}$. $\therefore\angle DAE=\angle DAC - \angle EAC = 20^{\circ}$. $\therefore\angle DEA = 90^{\circ}-\angle DAE = 90^{\circ}-20^{\circ}=70^{\circ}$.
2. 新视角 探究题 (1) 如图①,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY,XZ恰好分别经过点B,C. 在△ABC中,∠A = 30°,则∠ABC + ∠ACB = ________,∠XBC + ∠XCB = ________;
(2)在(1)的条件下,如图②,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX + ∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX + ∠ACX的大小.

(2)在(1)的条件下,如图②,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX + ∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX + ∠ACX的大小.

答案:
【解】
(1)$150^{\circ};90^{\circ}$
(2)不变化. $\because\angle A = 30^{\circ},\therefore\angle ABC+\angle ACB = 150^{\circ}$. $\because\angle X = 90^{\circ},\therefore\angle XBC+\angle XCB = 90^{\circ}$. $\therefore\angle ABX+\angle ACX = (\angle ABC - \angle XBC)+(\angle ACB - \angle XCB)=(\angle ABC+\angle ACB)-(\angle XBC+\angle XCB)=150^{\circ}-90^{\circ}=60^{\circ}$.
(1)$150^{\circ};90^{\circ}$
(2)不变化. $\because\angle A = 30^{\circ},\therefore\angle ABC+\angle ACB = 150^{\circ}$. $\because\angle X = 90^{\circ},\therefore\angle XBC+\angle XCB = 90^{\circ}$. $\therefore\angle ABX+\angle ACX = (\angle ABC - \angle XBC)+(\angle ACB - \angle XCB)=(\angle ABC+\angle ACB)-(\angle XBC+\angle XCB)=150^{\circ}-90^{\circ}=60^{\circ}$.
3. [2024·滨州邹平市期末] 现有一张△ABC纸片,D,E分别是△ABC边上两点,若沿直线DE折叠,点A落在点A'处.
(1)如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是________;
(2)如果折成图②的形状,猜想∠1 + ∠2与∠A的数量关系是________;
(3)如果折成图③的形状,猜想∠1,∠2和∠A的数量关系,并说明理由.

(1)如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是________;
(2)如果折成图②的形状,猜想∠1 + ∠2与∠A的数量关系是________;
(3)如果折成图③的形状,猜想∠1,∠2和∠A的数量关系,并说明理由.

答案:
【解】
(1)$\angle 1 = 2\angle A$
(2)$\angle 1+\angle 2 = 2\angle A$ 【点拨】由折叠的性质得$\angle ADE=\angle A'DE,\angle AED=\angle A'ED$.$\because\angle ADB+\angle AEC = 360^{\circ}$, $\therefore\angle 1+\angle 2 = 360^{\circ}-\angle ADE-\angle A'DE-\angle AED-\angle A'ED = 360^{\circ}-2\angle ADE - 2\angle AED = 360^{\circ}-2(\angle ADE+\angle AED)$.$\because\angle ADE+\angle AED = 180^{\circ}-\angle A$, $\therefore\angle 1+\angle 2 = 2\angle A$.
(3)$\angle 2-\angle 1 = 2\angle A$.理由如下:如图, $\because\angle 2=\angle AFE+\angle A,\angle AFE=\angle A'+\angle 1$,由折叠的性质得$\angle A=\angle A'$.$\therefore\angle 2=\angle A'+\angle 1+\angle A = 2\angle A+\angle 1$.$\therefore\angle 2-\angle 1 = 2\angle A$.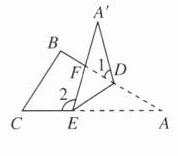
【解】
(1)$\angle 1 = 2\angle A$
(2)$\angle 1+\angle 2 = 2\angle A$ 【点拨】由折叠的性质得$\angle ADE=\angle A'DE,\angle AED=\angle A'ED$.$\because\angle ADB+\angle AEC = 360^{\circ}$, $\therefore\angle 1+\angle 2 = 360^{\circ}-\angle ADE-\angle A'DE-\angle AED-\angle A'ED = 360^{\circ}-2\angle ADE - 2\angle AED = 360^{\circ}-2(\angle ADE+\angle AED)$.$\because\angle ADE+\angle AED = 180^{\circ}-\angle A$, $\therefore\angle 1+\angle 2 = 2\angle A$.
(3)$\angle 2-\angle 1 = 2\angle A$.理由如下:如图, $\because\angle 2=\angle AFE+\angle A,\angle AFE=\angle A'+\angle 1$,由折叠的性质得$\angle A=\angle A'$.$\therefore\angle 2=\angle A'+\angle 1+\angle A = 2\angle A+\angle 1$.$\therefore\angle 2-\angle 1 = 2\angle A$.

查看更多完整答案,请扫码查看


