《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

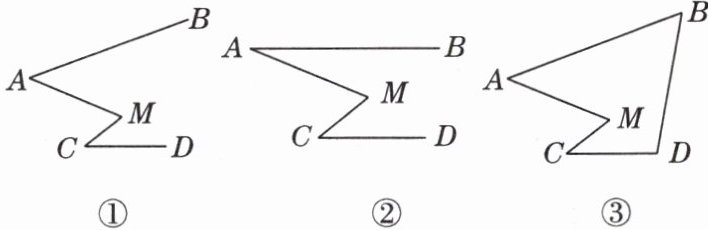
4. 如图①，由线段BA，AM，MC，CD组成的图形 ，称为“ 形BAMCD”.
(1)如图②，在 形BAMCD中，若AB//CD，∠AMC = 60°，则∠A + ∠C = ________°.
(2)如图③，连接 形BAMCD中的B，D两点，若∠B + ∠D = 160°，∠AMC = α，试猜想∠A与∠C的数量关系，并说明理由.

答案：
【解】
(1)$60$
(2)$\angle A+\angle C = 20^{\circ}+\alpha$. 理由如下：如图，过点$A$作$AK\parallel CD$交$BD$于点$K$，则$\angle AKB=\angle D$. $\because\angle B+\angle D = 160^{\circ}$, $\therefore\angle B+\angle AKB = 160^{\circ}$. $\therefore\angle BAK = 180^{\circ}-160^{\circ}=20^{\circ}$. 由
(1)得$\angle AMC=\angle KAM+\angle C$. $\because\angle AMC=\alpha,\therefore\angle BAM+\angle C=\angle BAK+\angle KAM+\angle C = 20^{\circ}+\angle AMC = 20^{\circ}+\alpha$.

5. 如图，求∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7的度数.

答案： 【解】连接$CG,DF$. 在$\triangle COG$和$\triangle AOB$中，$\angle COG=\angle AOB$, $\therefore\angle 6+\angle 7=\angle OCG+\angle OGC$. 在四边形$CDFG$中，易知$\angle OCG+\angle 2+\angle CDF+\angle DFG+\angle 3+\angle OGC = 360^{\circ}$, 即$\angle 2+\angle 3+\angle 6+\angle 7+\angle CDF+\angle DFG = 360^{\circ}$. 在$\triangle DEF$中，$\angle EDF+\angle EFD+\angle 5 = 180^{\circ}$, $\therefore\angle EDF+\angle CDF+\angle EFD+\angle DFG+\angle 2+\angle 3+\angle 5+\angle 6+\angle 7 = 540^{\circ}$, 即$\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7 = 540^{\circ}$. 

6. 如图，AD平分∠BAC，∠EAD = ∠EDA.
(1)求证：∠EAC = ∠B.
(2)若∠B = 50°，∠CAD : ∠E = 1 : 3，求∠E的度数.

答案：  
(1)【证明】$\because AD$平分$\angle BAC,\therefore\angle BAD=\angle CAD$. 又$\because\angle EAD=\angle EDA,\angle EAC=\angle EAD - \angle CAD,\angle B=\angle EDA - \angle BAD,\therefore\angle EAC=\angle B$.
(2)【解】设$\angle CAD = x,\because\angle CAD:\angle E = 1:3$, $\therefore\angle E = 3x$, 由
(1)知$\angle EAC=\angle B = 50^{\circ}$, $\therefore\angle EAD=\angle EDA = x + 50^{\circ}$. 在$\triangle EAD$中，$\because\angle E+\angle EAD+\angle EDA = 180^{\circ}$, $\therefore 3x+2(x + 50^{\circ}) = 180^{\circ}$, 解得$x = 16^{\circ}$.$\therefore 3x = 48^{\circ}$,即$\angle E = 48^{\circ}$. 

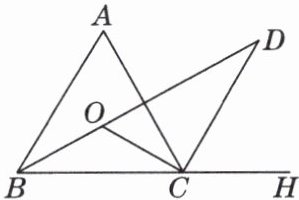
7. 如图，在△ABC中，∠ABC的平分线和∠ACB的平分线交于点O，D是外角∠ACH的平分线与内角∠ABC的平分线的交点，∠BOC = 120°.
(1)求∠A的度数；
(2)求∠D的度数.

答案： 【解】
(1)$\because\angle BOC = 120^{\circ},\therefore\angle OBC+\angle OCB = 60^{\circ}$. $\because\angle ABC$的平分线和$\angle ACB$的平分线交于点$O$, $\therefore\angle ABC = 2\angle OBC,\angle ACB = 2\angle OCB$. $\therefore\angle ABC+\angle ACB = 2\angle OBC+2\angle OCB = 2(\angle OBC+\angle OCB)=120^{\circ}$.$\therefore\angle A = 180^{\circ}-(\angle ABC+\angle ACB)=60^{\circ}$.
(2)$\because D$是外角$\angle ACH$的平分线与内角$\angle ABC$的平分线的交点，$\therefore\angle DCH=\frac{1}{2}\angle ACH,\angle DBC=\frac{1}{2}\angle ABC$. $\therefore\angle D=\angle DCH - \angle DBC=\frac{1}{2}(\angle ACH - \angle ABC)=\frac{1}{2}\angle A = 30^{\circ}$.