《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

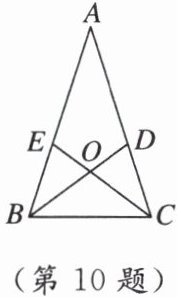
10. 如图，在 $\triangle ABC$ 中，$AB = AC$，$\angle A = 36^{\circ}$，$BD$，$CE$ 分别是 $\angle ABC$，$\angle ACB$ 的平分线，则图中的等腰三角形有 （ ）
A. $5$ 个 B. $6$ 个 C. $7$ 个 D. $8$ 个

答案： D@@【点拨】 - 在△ABC中，AB = AC，∠A = 36°，所以△ABC是等腰三角形，∠ABC = ∠ACB = $\frac{1}{2}$×(180° - 36°) = 72°。 - 因为BD，CE分别是∠ABC与∠ACB的平分线，所以∠ABD = ∠CBD = ∠ACE = ∠BCE = 36° = ∠A。 - 所以AE = CE，AD = BD，BO = CO，所以△ABD，△ACE，△BOC是等腰三角形。 - 因为∠BEC = 180° - ∠ABC - ∠BCE = 72°，∠CDB = 180° - ∠BCD - ∠CBD = 72°，∠EOB = ∠DOC = ∠CBD + ∠BCE = 72°，所以∠BEO = ∠BOE = ∠ABC = ∠ACB = ∠CDO = ∠COD，所以BE = BO，CO = CD，BC = BD = CE，所以△BEO，△CDO，△BCD，△CBE是等腰三角形，所以图中的等腰三角形有8个，故选D。

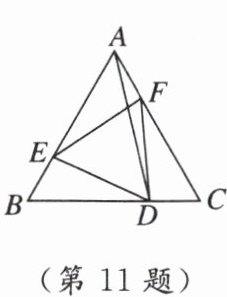
11. 如图，在 $\triangle ABC$ 中，$AB = AC$，$D$ 是 $BC$ 上的一点，在 $AB$，$AC$ 上分别截取 $BE = CD$，$CF = BD$，连接 $DE$，$DF$，$EF$，$AD$. 有下列结论：
①$\angle EDF = 90^{\circ} - \frac{1}{2} \angle BAC$；② $\angle EDF = \angle B$；③$AD \perp BC$；④$\angle DEF = \angle DFE$. 其中正确结论的序号是 （ ）

A. ①②
B. ②④
C. ①②③
D. ①②④

答案： D@@【点拨】 - 在△ABC中，AB = AC，所以∠B = ∠C = $\frac{1}{2}(180° - ∠BAC)=90°-\frac{1}{2}∠BAC$。 - 在△BDE和△CFD中，$\begin{cases}BE = CD\\∠B = ∠C\\BD = CF\end{cases}$，所以△BDE≌△CFD(SAS)。 - 所以DE = DF，∠BED = ∠CDF。 - 因为∠BDE + ∠EDF + ∠CDF = 180°，所以∠EDF = 180° - (∠BDE + ∠CDF) = 180° - (∠BDE + ∠BED)。 - 因为∠BDE + ∠BED = 180° - ∠B，所以∠EDF = 180° - (180° - ∠B) = ∠B = 90° - $\frac{1}{2}∠BAC$。 - 故①②正确；因为DE = DF，所以∠DEF = ∠DFE，故④正确。 - 因为AB = AC，当AD⊥BC时，BD = CD。根据题意，可知D是BC上的一点，但BD，CD不一定相等，所以AD，BC不一定垂直，故③错误。综上所述，正确的有①②④，故选D。

12. 如图，在 $\triangle ABC$ 中，$AB = AC$，$AE$ 是 $BC$ 边上的高，$\angle ABC$ 的平分线与 $AE$ 相交于点 $D$，求证：点 $D$ 在 $\angle ACB$ 的平分线上.

答案： 【证明】 - 连接CD。因为AB = AC，所以∠ABC = ∠ACB。 - 因为AE是BC边上的高，所以BE = CE，∠DEB = ∠DEC = 90°。 - 又因为DE = DE，所以△DEB≌△DEC(SAS)，所以∠DBE = ∠DCE，易得∠ABD = ∠ACD。 - 因为∠ABC的平分线与AE相交于点D，所以∠ABD = ∠DBC，所以∠ACD = ∠DCE，所以点D在∠ACB的平分线上。

13. (1) 如图①，在 $\triangle ABC$ 中，$AB = AC$，$\angle BAC = 45^{\circ}$. $\triangle ABC$ 的高 $AD$，$BE$ 相交于点 $M$. 求证：$AM = 2CD$；
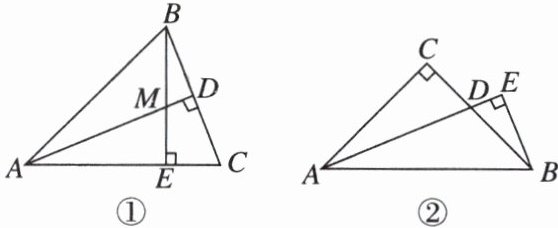
(2) 如图②，在 $Rt\triangle ABC$ 中，$\angle C = 90^{\circ}$，$AC = BC$，$AD$ 是 $\angle CAB$ 的平分线，过点 $B$ 作 $BE \perp AD$，交 $AD$ 的延长线于点 $E$. 若 $AD = 3$，求 $BE$ 的长.

答案：
-
(1)【证明】 - 因为BE是△ABC的高，所以∠AEB = ∠BEC = 90°，所以∠ABE = 90° - ∠BAE = 45° = ∠BAE，所以AE = BE。 - 因为AD是△ABC的高，所以∠ADC = 90°，所以∠EAM = 90° - ∠C = ∠EBC。 - 在△AEM和△BEC中，$\begin{cases}∠EAM = ∠EBC\\AE = BE\\∠AEM = ∠BEC\end{cases}$，所以△AEM≌△BEC(ASA)，所以AM = BC。 - 因为AB = AC，AD⊥BC，所以BD = CD，所以BC = 2CD，所以AM = 2CD。 -
(2)【解】 - 如图，延长BE，AC交于点F。 - 因为BE⊥EA，所以∠AEF = ∠AEB = 90°。 - 因为AD平分∠BAC，所以∠FAE = ∠BAE，易得∠F = ∠ABE，所以AF = AB，所以BE = EF = $\frac{1}{2}BF$。 - 因为AC = BC，∠C = 90°，所以∠CAB = 45°，∠BCF = 90°，所以∠AFE = (180° - 45°)÷2 = 67.5°，∠FAE = 45°÷2 = 22.5°，所以∠CDA = 180° - 90° - 22.5° = 67.5°。 - 在△ADC和△BFC中，$\begin{cases}∠ADC = ∠F = 67.5°\\∠ACD = ∠BCF = 90°\\AC = BC\end{cases}$，所以△ADC≌△BFC(AAS)，所以AD = BF，所以BE = $\frac{1}{2}AD$ = 1.5。