《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

1. 真实情境题 航天科技 2024年10月30日，搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉发射取得圆满成功，3名航天员顺利进驻中国空间站. 如图①是中国空间站上机械臂的一种工作状态，且两臂相等，抽象为数学问题如图②，AB，AC是两臂，且AB = AC，若两臂的夹角∠BAC = 100°时，连接BC，则∠B的度数为 （ ）

A. 40°
B. 50°
C. 60°
D. 80°

答案： A

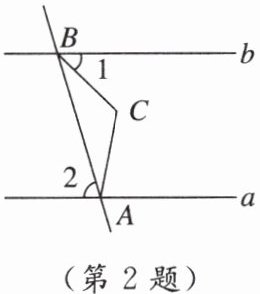
2. 如图，直线a//b，点A在直线a上，点B在直线b上，AC = BC，∠C = 120°，∠1 = 44°，则∠2的度数为 （ ）

A. 64°
B. 74°
C. 56°
D. 66°

答案： B

3. [2024·济南模拟] 如图，在某滑雪场滑雪时，需从山脚处乘缆车上山，缆车索道与水平线所成的角为30°，缆车速度为每分钟40米，缆车从山脚处A到达山顶处B需要15分钟，则山的高度BC为 （ ）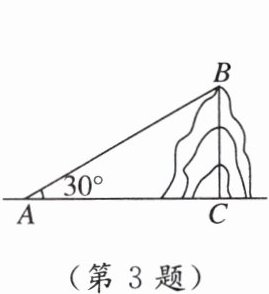
A. 300√3米
B. 600√3米
C. 300米
D. 1 200米

答案： C

4. 若△ABC的三边长分别是a，b，c，则下列条件：①∠A + ∠B = ∠C；②a : b : c = 5 : 12 : 13；③∠A : ∠B : ∠C = 3 : 4 : 5；④b² = (a + c)(a - c)中不能判定△ABC是直角三角形的个数有 （ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： A

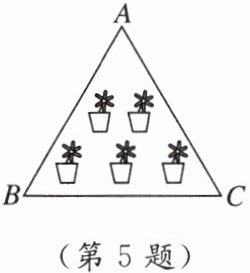
5. 如图，计划在一块等边三角形的空地上种植花卉，以美化环境. 若AB = 10 m，则这块等边三角形空地的面积为 （ ）

A. $\frac{\sqrt{75}}{2}$ m²
B. $\sqrt{75}$ m²
C. 5$\sqrt{75}$ m²
D. 10$\sqrt{75}$ m²

答案： C

6. [2024·德州期中] 如图，在△ABC和△DEC中，已知AB = DE，∠B = ∠E，添加一个条件，不能判定△ABC≌△DEC的是 （ ）
A. AC = DC
B. BC = EC
C. ∠A = ∠D
D. ∠ECB = ∠DCA

答案： A

7. 命题“两直线平行，同旁内角互补”的逆命题为________________________.

答案： 同旁内角互补，两直线平行

8. [2024·德州 新情境 条件开放题] 如图，C是AB的中点，CD = BE，请添加一个条件：________，使△ACD≌△CBE.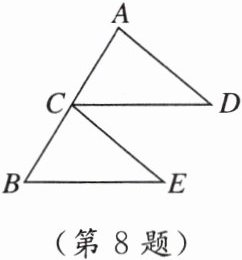

答案： AD = CE（答案不唯一）

9. [2024·东营期末] 腰长为4a，底角为15°的等腰三角形的面积为________.

答案： $4a^{2}$

10. 如图，在长方形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于点F，若CF = 1，FD = 2，则BC的长为________.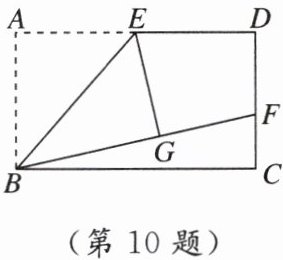

答案：
$\sqrt{24}$ 【点拨】连接 EF，如图。 则在长方形 ABCD 中， 根据翻折的性质和 E 是 AD 的中点，可得 BG = AB，∠EGB = ∠A = 90°，EG = AE = ED。 在 Rt△EGF 与 Rt△EDF 中，$\begin{cases}EG = ED \\ EF = EF\end{cases}$，
∴ Rt△EGF≌Rt△EDF（HL）.
∴ FG = FD.
∵ CF = 1，FD = 2，
∴ AB = CD = CF + FD = 1 + 2 = 3， FG = FD = 2.
∴ BG = AB = 3.
∴ BF = BG + FG = 3 + 2 = 5. 在 Rt△BCF 中，BC = $\sqrt{BF^{2}-CF^{2}}=\sqrt{5^{2}-1^{2}}=\sqrt{24}$

11. 如图，△ABC是等边三角形，高AD = 6，P为AD上一动点，E为AB的中点，则PB + PE的最小值为________.

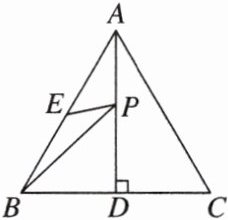
答案：
6 【点拨】
∵△ABC 为等边三角形，AD 为高，
∴ B，C 两点关于直线 AD 对称。 如图，连接 CE，CE 交 AD 于点 P，此时 易知线段 CE 的长即为 PB + PE 的最小值。
∵ E 为 AB 的中点，
∴ CE⊥AB，即 CE 为△ABC 的高线。
∴ CE = AD = 6.
∴ PB + PE 的最小值为 6