第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
11. [2024·枣庄薛城区期中] 如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,连接AE,分别以点E和点C为圆心,大于$\frac{1}{2}$EC的长为半径作弧,两弧相交于点P,作射线AP交BC于点D. 若∠B = 45°,∠ACE = 2∠CAD,则∠BAE的度数为( )
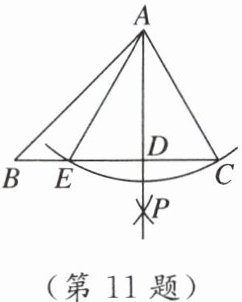
A. 15°
B. 25°
C. 30°
D. 35°
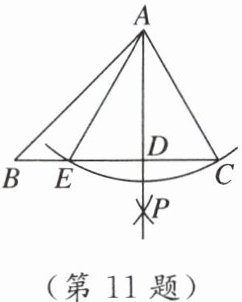
A. 15°
B. 25°
C. 30°
D. 35°
答案:
A
12. 如图,以等腰直角三角形ABC的直角边AC为边作等边三角形ACD,CE⊥AD于点E,BD,CE交于点F,则下列结论中正确的有________.(填序号)
①∠DFE = 45°;
②BC = 2DE;
③BF = 2DF;
④AB = 2DF.

①∠DFE = 45°;
②BC = 2DE;
③BF = 2DF;
④AB = 2DF.

答案:
①②④
13. 如图,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP = ∠ACQ,BP = CQ,问△APQ是什么形状的三角形?并证明你的结论.


答案:
【解】△APQ 为等边三角形. 证明如下:
∵△ABC 为等边三角形,
∴AB = AC,∠BAC = 60°. 在△ABP 和△ACQ 中,AB = AC,∠ABP = ∠ACQ,BP = CQ,
∴△ABP≌△ACQ(SAS).
∴AP = AQ,∠BAP = ∠CAQ.
∵∠BAC = ∠BAP + ∠PAC = 60°,
∴∠PAQ = ∠CAQ + ∠PAC = 60°.
∴△APQ 是等边三角形.
∵△ABC 为等边三角形,
∴AB = AC,∠BAC = 60°. 在△ABP 和△ACQ 中,AB = AC,∠ABP = ∠ACQ,BP = CQ,
∴△ABP≌△ACQ(SAS).
∴AP = AQ,∠BAP = ∠CAQ.
∵∠BAC = ∠BAP + ∠PAC = 60°,
∴∠PAQ = ∠CAQ + ∠PAC = 60°.
∴△APQ 是等边三角形.
14. 学科素养 几何直观 等边三角形ABC的边长为9,P是AB上一动点,点P以每秒1个单位长度的速度从点A向点B运动,设运动时间为t秒.
(1)如图①,点Q是BC上一点,若BQ = 6,PQ//AC,求t的值.
(2)如图②,若点P从点A向点B运动,同时动点Q以每秒2个单位长度的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形?
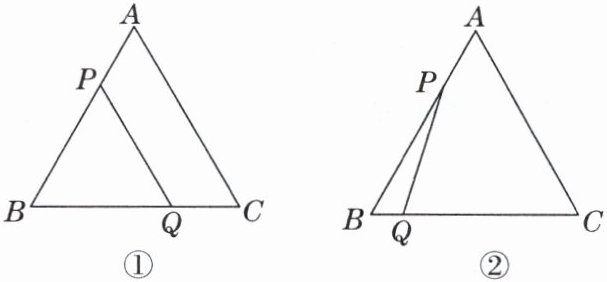
(1)如图①,点Q是BC上一点,若BQ = 6,PQ//AC,求t的值.
(2)如图②,若点P从点A向点B运动,同时动点Q以每秒2个单位长度的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形?

答案:
【解】
(1)
∵△ABC 是等边三角形,PQ∥AC,
∴∠BQP = ∠C = 60°,∠BPQ = ∠A = 60°,∠B = 60°.
∴∠B = ∠BQP = ∠BPQ = 60°.
∴△BPQ 是等边三角形.
∴BP = BQ = 6. 由题意知 AP = t,则 BP = 9 - t,
∴9 - t = 6,解得 t = 3.
(2)①当点 Q 在边 BC 上时,易知△APQ 不可能为等边三角形; ②当点 Q 在边 AC 上时,若△APQ 为等边三角形,则 AP = AQ. 由题意知 AP = t,BC + CQ = 2t,
∴AQ = BC + AC - (BC + CQ) = 9 + 9 - 2t = 18 - 2t.
∴18 - 2t = t,解得 t = 6.
∴当 t = 6 时,△APQ 为等边三角形.
(1)
∵△ABC 是等边三角形,PQ∥AC,
∴∠BQP = ∠C = 60°,∠BPQ = ∠A = 60°,∠B = 60°.
∴∠B = ∠BQP = ∠BPQ = 60°.
∴△BPQ 是等边三角形.
∴BP = BQ = 6. 由题意知 AP = t,则 BP = 9 - t,
∴9 - t = 6,解得 t = 3.
(2)①当点 Q 在边 BC 上时,易知△APQ 不可能为等边三角形; ②当点 Q 在边 AC 上时,若△APQ 为等边三角形,则 AP = AQ. 由题意知 AP = t,BC + CQ = 2t,
∴AQ = BC + AC - (BC + CQ) = 9 + 9 - 2t = 18 - 2t.
∴18 - 2t = t,解得 t = 6.
∴当 t = 6 时,△APQ 为等边三角形.
查看更多完整答案,请扫码查看


