第102页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
10. 如图,$a,b,c$是数轴上三个点$A,B,C$所对应的实数.
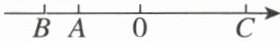
(1)将$a,b,c,0$由大到小排列:________________(用“>”连接);
(2)$a - b$______0;$b - c$______0(填“>”“=”或“<”);
(3)试化简:$-|a - b|+\sqrt[3]{(a + c)^{3}}-\sqrt{(c - b)^{2}}$.
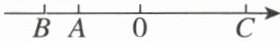
(1)将$a,b,c,0$由大到小排列:________________(用“>”连接);
(2)$a - b$______0;$b - c$______0(填“>”“=”或“<”);
(3)试化简:$-|a - b|+\sqrt[3]{(a + c)^{3}}-\sqrt{(c - b)^{2}}$.
答案:
【解】
(1)$c>0>a>b$
(2)>;<
(3)$\because a - b>0$,$c - b>0$, $\therefore -|a - b|+\sqrt[3]{(a + c)^{3}}-\sqrt{(c - b)^{2}}=-(a - b)+(a + c)-(c - b)=-a + b+a + c - c + b=2b$.
(1)$c>0>a>b$
(2)>;<
(3)$\because a - b>0$,$c - b>0$, $\therefore -|a - b|+\sqrt[3]{(a + c)^{3}}-\sqrt{(c - b)^{2}}=-(a - b)+(a + c)-(c - b)=-a + b+a + c - c + b=2b$.
11. [新考法作差法]根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若$a - b>0$,则$a>b$;若$a - b = 0$,则$a = b$;若$a - b<0$,则$a<b$.反之也成立.这种比较大小的方法称为“作差法”.请运用这种方法尝试解决下面的问题:
(1)比较$4 + 3a^{2}-2b + b^{2}$与$3a^{2}-2b + 1$的大小;
(2)若$2a + 2b>3a + b$,比较$a,b$的大小.
(1)比较$4 + 3a^{2}-2b + b^{2}$与$3a^{2}-2b + 1$的大小;
(2)若$2a + 2b>3a + b$,比较$a,b$的大小.
答案:
【解】
(1)$4 + 3a^{2}-2b + b^{2}-(3a^{2}-2b + 1)=4 + 3a^{2}-2b + b^{2}-3a^{2}+2b - 1=b^{2}+3>0$, $\therefore 4 + 3a^{2}-2b + b^{2}>3a^{2}-2b + 1$.
(2)$\because 2a + 2b>3a + b$,$\therefore (2a + 2b)-(3a + b)>0$. $\therefore 2a + 2b-3a - b>0$. $\therefore -a + b>0$. $\therefore a < b$.
(1)$4 + 3a^{2}-2b + b^{2}-(3a^{2}-2b + 1)=4 + 3a^{2}-2b + b^{2}-3a^{2}+2b - 1=b^{2}+3>0$, $\therefore 4 + 3a^{2}-2b + b^{2}>3a^{2}-2b + 1$.
(2)$\because 2a + 2b>3a + b$,$\therefore (2a + 2b)-(3a + b)>0$. $\therefore 2a + 2b-3a - b>0$. $\therefore -a + b>0$. $\therefore a < b$.
12. [新视角项目探究题]【提出问题】已知$x - y = 2$,且$x>1,y<0$,试确定$x + y$的取值范围.
【分析问题】先根据已知条件用$y$去表示$x$,然后根据题中已知$x$的取值范围,构建$y$的不等式,从而确定$y$的取值范围,同理再确定$x$的取值范围,最后利用不等式的性质即可解决问题.
【解决问题】解:$\because x - y = 2,\therefore x = y + 2$.
$\because x>1,\therefore y + 2>1.\therefore y>-1$.
$\because y<0,\therefore -1<y<0$.①
同理,得$1<x<2$.②
由①+②,得$-1 + 1<y + x<0 + 2$,
$\therefore x + y$的取值范围是$0<x + y<2$.
【尝试应用】(1)已知$x - y = -3$,且$x<-1,y>1$,求$x + y$的取值范围;
(2)已知$y>1,x<-1$,若$x - y = a$成立,求$x + y$的取值范围(结果用含$a$的式子表示).
【分析问题】先根据已知条件用$y$去表示$x$,然后根据题中已知$x$的取值范围,构建$y$的不等式,从而确定$y$的取值范围,同理再确定$x$的取值范围,最后利用不等式的性质即可解决问题.
【解决问题】解:$\because x - y = 2,\therefore x = y + 2$.
$\because x>1,\therefore y + 2>1.\therefore y>-1$.
$\because y<0,\therefore -1<y<0$.①
同理,得$1<x<2$.②
由①+②,得$-1 + 1<y + x<0 + 2$,
$\therefore x + y$的取值范围是$0<x + y<2$.
【尝试应用】(1)已知$x - y = -3$,且$x<-1,y>1$,求$x + y$的取值范围;
(2)已知$y>1,x<-1$,若$x - y = a$成立,求$x + y$的取值范围(结果用含$a$的式子表示).
答案:
【解】
(1)$\because x - y=-3$,$\therefore x=y - 3$. $\because x < - 1$,$\therefore y - 3 < - 1$. $\therefore y < 2$. $\because y>1$, $\therefore 1 < y < 2$. ① 同理,得$-2 < x < - 1$. ② 由①+②,得$-2 + 1 < x + y < - 1+2$, $\therefore x + y$的取值范围是$-1 < x + y < 1$.
(2)$\because y>1$,$x < - 1$,$\therefore x - y < - 2$. $\because x - y=a$,$\therefore a < - 2$. $\because x - y=a$,$\therefore x=y + a$. $\because x < - 1$, $\therefore y + a < - 1$,$\therefore y < - 1 - a$. 又$\because y>1$,$\therefore 1 < y < - 1 - a$. ① 同理,得$a + 1 < x < - 1$. ② 由①+②,得$a + 2 < x + y < - 2 - a$, $\therefore$当$a < - 2$时,$x + y$的取值范围是$a + 2 < x + y < - 2 - a$.
(1)$\because x - y=-3$,$\therefore x=y - 3$. $\because x < - 1$,$\therefore y - 3 < - 1$. $\therefore y < 2$. $\because y>1$, $\therefore 1 < y < 2$. ① 同理,得$-2 < x < - 1$. ② 由①+②,得$-2 + 1 < x + y < - 1+2$, $\therefore x + y$的取值范围是$-1 < x + y < 1$.
(2)$\because y>1$,$x < - 1$,$\therefore x - y < - 2$. $\because x - y=a$,$\therefore a < - 2$. $\because x - y=a$,$\therefore x=y + a$. $\because x < - 1$, $\therefore y + a < - 1$,$\therefore y < - 1 - a$. 又$\because y>1$,$\therefore 1 < y < - 1 - a$. ① 同理,得$a + 1 < x < - 1$. ② 由①+②,得$a + 2 < x + y < - 2 - a$, $\therefore$当$a < - 2$时,$x + y$的取值范围是$a + 2 < x + y < - 2 - a$.
查看更多完整答案,请扫码查看


