《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

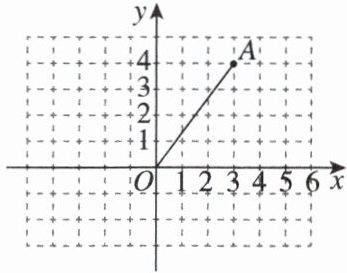
10. 新趋势 学科内综合 在如图所示的方格纸中，建立直角坐标系，点 A 的坐标为（3，4）.
（1）求 OA 的长；
（2）若△OAB 是以 OA 为腰的等腰三角形，点 B 为格点且点 B 在 x 轴上，求满足条件的点 B 的坐标.

答案： 【解】
(1)过点A作AH⊥x轴于点H，则OH = 3，AH = 4， 在Rt△AOH中，OA = $\sqrt{OH^{2}+AH^{2}}=\sqrt{3^{2}+4^{2}} = 5$.
(2)①若OA = AB，则BH = OH = 3.
∴OB = 2OH = 6，则点B的坐标为(6，0)；②若OA = OB，则OB = 5，
∴点B的坐标为(5，0)或(-5，0).
∴符合条件的点B的坐标为(6，0)或(5，0)或(-5，0).

11. [2024·常州] 如图，B，E，C，F 是直线 l 上的四点，AC，DE 相交于点 G，AB = DF，AC = DE，BC = EF.
（1）求证：△GEC 是等腰三角形；
（2）连接 AD，则 AD 与直线 l 的位置关系是_______.

答案：
(1)【证明】在△ABC和△DFE中，AB = DF，AC = DE，BC = FE，
∴△ABC≌△DFE.
∴∠ACB = ∠DEF.
∴EG = CG.
∴△GEC是等腰三角形.
(2)AD//直线l

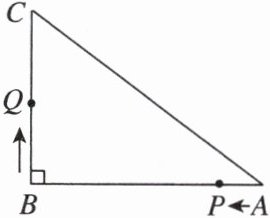
12. 新视角 动点探究题 如图，在△ABC 中，∠B = 90°，AB = 16 cm，BC = 12 cm，AC = 20 cm，P，Q 是△ABC 边上的两个动点，其中点 P 从点 A 开始沿 A→B 的方向运动，且速度为 1 cm/s，点 Q 从点 B 开始沿 B→C→A 的方向运动，且速度为 2 cm/s，它们同时出发，设出发的时间为 t s.
（1）BP = ________（用 t 的代数式表示）.
（2）当点 Q 在边 BC 上运动时，出发 ________ s 后，△PQB 是等腰三角形.
（3）当点 Q 在边 CA 上运动时，出发几秒后，△BCQ 是等腰三角形？

答案：
【解】
(1)(16 - t)cm
(2)$\frac{16}{3}$ 【点拨】当点Q在边BC上运动，且△PQB为等腰三角形时，有BP = BQ，即16 - t = 2t，解得t = $\frac{16}{3}$，
∴出发$\frac{16}{3}$ s后，△PQB是等腰三角形.
(3)①当△BCQ是以BC为底边的等腰三角形时，CQ = BQ，如图①，则∠C = ∠CBQ.
∵∠ABC = 90°，
∴∠CBQ + ∠ABQ = 90°，∠A + ∠C = 90°.
∴∠A = ∠ABQ.
∴BQ = AQ.
∴易得CQ = AQ = 10 cm.
∴BC + CQ = 22 cm.
∴t = 22÷2 = 11； ②当△BCQ是以BQ为底边的等腰三角形时，CQ = BC = 12 cm，如图②，则BC + CQ = 24 cm，
∴t = 24÷2 = 12； ③当△BCQ是以CQ为底边的等腰三角形时，BQ = BC，如图③，过点B作BD⊥AC于点D，则CD = DQ.
∵$\frac{1}{2}$AB·BC = $\frac{1}{2}$AC·BD， 即$\frac{1}{2}$×16×12 = $\frac{1}{2}$×20BD，
∴BD = $\frac{48}{5}$.
∴CD = $\sqrt{BC^{2}-BD^{2}}=\frac{36}{5}$.
∴CQ = 2CD = $\frac{72}{5}$.
∴BC + CQ = 12+$\frac{72}{5}=\frac{132}{5}$.
∴t = $\frac{132}{5}$÷2 = $\frac{66}{5}$. 综上所述，当点Q在边CA上运动时，出发11 s或12 s或$\frac{66}{5}$ s后，△BCQ是等腰三角形.