《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

1. 如图，在△ABC 中，∠ACB = 90°，∠CAB = 35°，将△ABC 沿 AB 边所在直线翻折得△ABC'，连接 CC'交 AB 于点 D，则∠BC'C 的度数为 （ ）

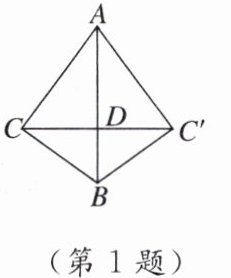
A. 35°
B. 45°
C. 55°
D. 65°

答案： A

2. 情境题 生活应用 如图，小明和小红玩跷跷板游戏，跷跷板的支点 O（即跷跷板的中点）到地面的距离是 50 cm. 当小红从水平位置 CD 下降 30 cm 时，小明离地面的高度是 ________.

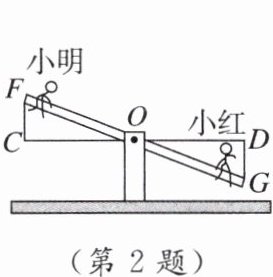
答案： 80 cm

3. 如图，已知 AC = AB，AE = AD，∠EAB = ∠DAC，求证：CE = BD.

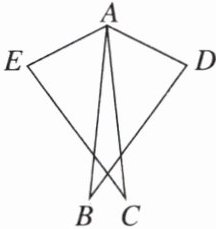
答案： 【证明】 因为∠EAB = ∠DAC，∠BAC = ∠CAB，所以∠EAC = ∠DAB。 在△EAC和△DAB中， $\begin{cases} AC = AB \\ \angle EAC = \angle DAB \\ AE = AD \end{cases}$所以△EAC≌△DAB(SAS)，所以CE = BD。

4. 新考法 等线段代换法 如图，AB⊥CD，且 AB = CD. E，F 是 AD 上两点，CE⊥AD，BF⊥AD. 若 CE = a，BF = b，EF = c，则 AD 的长为 （ ）

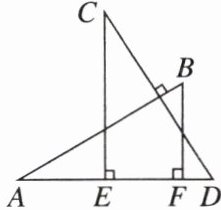
A. a + c
B. b + c
C. a - b + c
D. a + b - c

答案： D@@【点拨】因为CE⊥AD，BF⊥AD，所以∠CED = ∠AFB = 90°。设BF交CD于点M，则∠BMC = ∠DMF，所以易知∠B = ∠D。 在△ABF和△CDE中， $\begin{cases}  \angle B = \angle D \\ \angle AFB = \angle CED \\ AB = CD \end{cases}$ 所以△ABF≌△CDE(AAS)。所以AF = CE = a，DE = BF = b。 所以DF = DE - EF = b - c。所以AD = AF + DF = a + b - c，故选D。

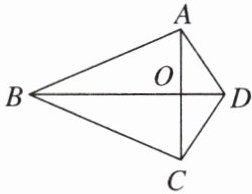
5. 新视角 新定义题 两组邻边分别相等的四边形叫做“筝形”. 如图，四边形 ABCD 是一个筝形，其中 AD = CD，AB = CB，AC，BD 交于点 O，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO = CO = $\frac{1}{2}$AC；③△ABD≌△CBD；④四边形 ABCD 的面积 = AC·BD. 其中正确的结论有 （ ）

A. 1 个
B. 2 个
C. 3 个
D. 4 个

答案： C@@【点拨】在△ABD与△CBD中， $\begin{cases} AD = CD \\ AB = BC \\ DB = DB  \end{cases}$\[ 所以△ABD≌△CBD(SSS)，故③正确；所以∠ADB = ∠CDB。 在△AOD与△COD中， $\begin{cases} AD = CD \\ \angle ADO = \angle CDO \\ OD = OD   \end{cases}$ 所以△AOD≌△COD(SAS)。所以∠AOD = ∠COD = 90°，AO = OC = $\frac{1}{2}AC$。所以AC⊥DB，故①②正确； 四边形ABCD的面积 = $S_{\triangle ADB}+S_{\triangle BDC}=\frac{1}{2}DB\times OA+\frac{1}{2}DB\times OC=\frac{1}{2}AC\cdot BD$，故④错误。故选C。

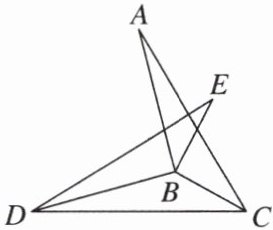
6. 如图，将两个三角形纸板△ABC 和△DBE 按如图所示的方式摆放，连接 DC. 已知∠DBA = ∠CBE，∠BAC = ∠BDE，AC = DE = DC.
（1）求证：△ABC≌△DBE.
（2）若∠ACD = 68°，求∠BED 的度数.

答案：
(1)【证明】因为∠DBA = ∠CBE， 所以∠DBA + ∠ABE = ∠CBE + ∠ABE，即∠DBE = ∠ABC。 在△ABC和△DBE中，$\begin{cases} \angle ABC = \angle DBE \\ \angle BAC = \angle BDE \\ AC = DE  \end{cases}$  所以△ABC≌△DBE(AAS)。
(2)【解】因为△ABC≌△DBE，所以BD = BA，∠BCA = ∠BED。 在△DBC和△ABC中$\begin{cases}DC = AC \\ CB = CB \\ BD = BA\end{cases}$  所以△DBC≌△ABC(SSS)。所以∠BCD = ∠BCA = $\frac{1}{2}\angle ACD$。 因为∠ACD = 68°，所以∠BCA = 34°。所以∠BED = ∠BCA = 34°。

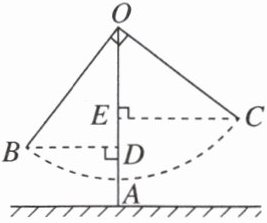
7. 张华与爸爸妈妈在公园里荡秋千，如图，张华坐在秋千的起始位置 A 处，OA 与地面垂直，两脚在地面上用力一蹬，妈妈在距地面 1.1 m 高的 B 处接住他后用力一推，爸爸在 C 处接住他. 若妈妈与爸爸到 OA 的水平距离 BD，CE 分别为 1.6 m 和 2 m，∠BOC = 90°.
（1）△OBD 与△COE 全等吗？请说明理由.
（2）爸爸是在距离地面多高的地方接住张华的？（提示：夹在两条平行线间的垂直线段都相等.）

答案： 【解】
(1)△COE≌△OBD。理由如下： 由题意可知∠CEO = ∠BDO = 90°，OB = OC。 因为∠BOC = 90°，所以∠COE + ∠BOD = 90° = ∠BOD + ∠OBD。 所以∠COE = ∠OBD。 在△COE和△OBD中， $\begin{cases} \angle COE = \angle OBD \\ \angle CEO = \angle ODB \\ OC = OB \end{cases}$所以△COE≌△OBD(AAS)。
(2)因为△COE≌△OBD，所以CE = OD，OE = BD。 因为BD = 1.6 m，CE = 2 m， 所以DE = OD - OE = CE - BD = 2 - 1.6 = 0.4(m)。 所以爸爸是在距离地面1.1 + 0.4 = 1.5(m)的地方接住张华的。