《2025年初中学霸创新题七年级数学下册北师大版》

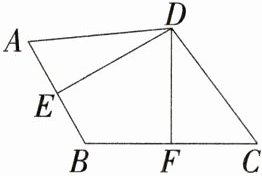
1 如图，DE，DF分别是线段AB，BC的垂直平分线，连接DA，DC，则 ( )

A. ∠A=∠C
B. ∠B=∠ADC
C. DA=DC
D. DE=DF

答案： C

2 新情境·生产生活 某地新建的丽苑新城小区的三个出口A，B，C的位置如图所示，小区物业计划在小区内修建一个智能电动汽车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该建在 ( )

A. 三条边的垂直平分线的交点处
B. 三个内角的平分线的交点处
C. 三角形三条高线的交点处
D. 三角形三条中线的交点处

答案： A

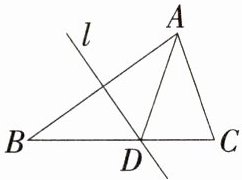
3 (山西晋中期末)如图，△ABC中，∠B=35°，AB边的垂直平分线l交BC于点D，连接AD。若BD=AC，则∠C的大小为 ( )

A. 65°
B. 70°
C. 75°
D. 80°

答案： B

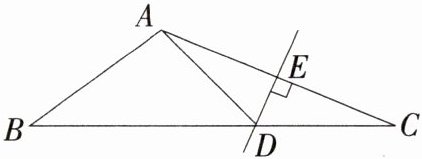
4 (河南平顶山宝丰县期末)如图，在△ABC中，AC的垂直平分线分别交BC，AC于点D，E。若AE=3 cm，△ABD的周长为13 cm，则△ABC的周长为________cm。

答案： 19

5 新趋势·过程性学习 如图所示，在△ABC中，AD是∠BAC的平分线，AD的垂直平分线分别交AB，BC延长线于点F，E。
试说明：DF//AC。
解：因为AD平分∠BAC，
所以∠________=∠________(角平分线的定义)。
因为EF垂直平分AD，
所以________=________(线段垂直平分线上的点到这条线段两个端点的距离相等)，
所以∠BAD=∠ADF(________________)，
所以∠DAC=∠ADF(等量代换)，
所以DF//AC(________________)。

答案： BAD@@DAC@@FD@@FA@@等边对等角@@内错角相等，两直线平行

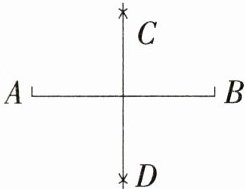
6 如图，已知线段AB=6，利用尺规作线段AB的垂直平分线，步骤如下：
①分别以点A，B为圆心，以b的长为半径作弧，两弧相交于点C和D；
②作直线CD。直线CD就是线段AB的垂直平分线。则b的长可能是 ( )

A. 1
B. 2
C. 3
D. 4

答案： D

7 如图，已知△ABC，AB＞AC。
(1)用尺规求作点P，点P在边AB上，且PB=PC(保留作图痕迹，不写作法)
(2)连接PC，若AB=6，AC=4，则△APC的周长是多少?

答案：