《2025年初中学霸创新题七年级数学下册北师大版》

1 (河南郑州经开区期末)若一个三角形的三边长分别为3,5,a，则a的值可能是 ( )
A. 2
B. 5
C. 8
D. 10

答案： B

2 如图，在△ABC中，BC边上的高为 ( )


A. BE
B. CF
C. BD
D. AF

答案： D

3 (山西晋中平遥县模拟)在实践活动中，李明和王刚进行角的探究，他们将一副三角尺按如图所示方式摆放，使有刻度的两边互相垂直，则∠1= ( )

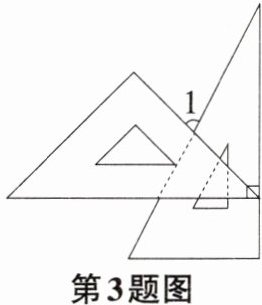
A. 45°
B. 60°
C. 50°
D. 75°

答案： D

4 (河南郑州中牟县期末)如图，AD是△ABC的中线，DE是△ADC的中线，若S△DCE=3，则S△ABC是 ( )


A. 12
B. 14
C. 16
D. 18

答案： A

5 如图，在△ABC中，AD,CE是三角形的高，若AB =5,BC=6,AD=4，则线段CE的长为 ( )

A. $\frac{24}{5}$
B. 4
C. 5
D. 6

答案： A

6 若a，b，c分别是△ABC三边的长，化简：|a+b -c|+|b -a -c| -|c -a -b|= ( )
A. a+b -c
B. a -b +c
C. b -a +c
D. 2a -b +c

答案： B

7 如图，∠MON=90°，点A,B分别在射线OM,ON上运动，BE平分∠NBA，BE的反向延长线与∠BAO的平分线交于点C。若已知∠BAO=45°，则∠C= ( )


A. 45°
B. 60°
C. 75°
D. 80°

答案： A

8 如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，给出以下结论：①BF=AF；②∠AFG=∠AGF；③∠FAG=2∠ACF；④S△ABE=S△BCE；⑤BH=CH；⑥AD·BC=AB·AC；⑦S△BHF=S△CHE。其中结论正确的有 ( )

A. 3个
B. 4个
C. 5个
D. 6个

答案： B

9 已知，在△ABC中，∠A=3∠B=6∠C，这个三角形按角来分是________三角形。

答案： 钝角

10 如图，在四边形ABCD中，AB=6，AD=4，BC=2，CD=10，则对角线BD的长度可能是________。(写出一个即可)

答案： 9（答案不唯一）

11 (河南信阳浉河区阶段练习)如图，AD是△ABC的中线，点E,F在AD上，且AE=EF=DF，连接BE,CF，若S△ABC=18，则阴影部分的面积为________。

答案： 6

12 新趋势 规律探究题 如图，在△ABC中，A1,A2,A3,⋯,An为边AC上不同的n个点，从B点首先连接BA1，图中有3个不同的三角形；再连接BA2，图中有6个不同的三角形……如此继续下去，连接BAn后，共有________个不同的三角形。

答案： $\frac{1}{2}(n + 1)(n + 2)$