第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11(9分)新趋势 过程性学习 请将下列解题过程补充完整(括号中填写推理的依据):
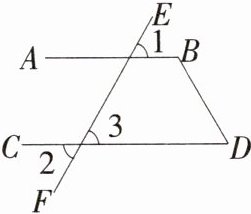
如图,已知∠1=∠2,∠D=60°,求∠B的度数。
解:因为∠1=∠2(已知),
∠2=∠3(__________),
所以∠3=∠1(等量代换),
所以________//________(__________),
所以∠D+∠B=180°(__________)。
又因为∠D=60°(已知),
所以∠B=________。

如图,已知∠1=∠2,∠D=60°,求∠B的度数。
解:因为∠1=∠2(已知),
∠2=∠3(__________),
所以∠3=∠1(等量代换),
所以________//________(__________),
所以∠D+∠B=180°(__________)。
又因为∠D=60°(已知),
所以∠B=________。
答案:
对顶角相等@@AB@@CD@@同位角相等,两直线平行@@两直线平行,同旁内角互补@@120°
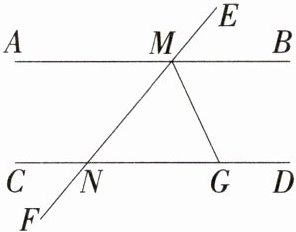
12(13分)如图,AB//CD,EF分别交AB,CD于点M,N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数。

答案:
解:因为∠EMB = 50°,所以∠BMF = 180° - 50° = 130°。
因为MG平分∠BMF,所以∠BMG = $\frac{1}{2}∠BMF = 65°$ 。
因为AB//CD,所以∠MGC = ∠BMG = 65°。
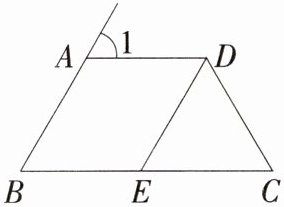
13(13分)(山西运城平陆县期末)如图,AD//BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E。
(1)求∠C的度数;
(2)试说明:AB//DE。
(1)求∠C的度数;
(2)试说明:AB//DE。

答案:
解:
(1)因为AD//BC,∠B = 60°,所以∠1 = ∠B = 60°。 因为∠1 = ∠C,所以∠C = ∠1 = 60°。
(2)因为AD//BC,∠C = 60°,所以∠ADC = 180° - ∠C = 120°。 因为DE平分∠ADC,所以∠ADE = $\frac{1}{2}∠ADC=\frac{1}{2}×120° = 60°$ , 所以∠1 = ∠ADE,所以AB//DE。
(1)因为AD//BC,∠B = 60°,所以∠1 = ∠B = 60°。 因为∠1 = ∠C,所以∠C = ∠1 = 60°。
(2)因为AD//BC,∠C = 60°,所以∠ADC = 180° - ∠C = 120°。 因为DE平分∠ADC,所以∠ADE = $\frac{1}{2}∠ADC=\frac{1}{2}×120° = 60°$ , 所以∠1 = ∠ADE,所以AB//DE。
14(15分)新趋势 探究性问题 综合与探究:
如图,一副三角尺,其中∠EDF=∠ACB=90°,∠E =45°,∠A=30°。
(1)若这副三角尺如图1所示摆放,EF//CD,求∠CDF的度数;
(2)将一副三角尺如图2所示摆放,直线GH//MN,保持三角尺ABC不动,现将三角尺DEF绕点D以每秒3°的速度顺时针旋转,设旋转时间为t s,且0≤t≤60,求当边BC与三角尺DEF的一条直角边(边DE,DF)平行时,所有满足条件的t的值。
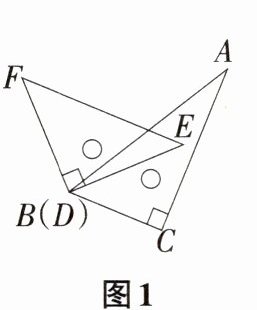
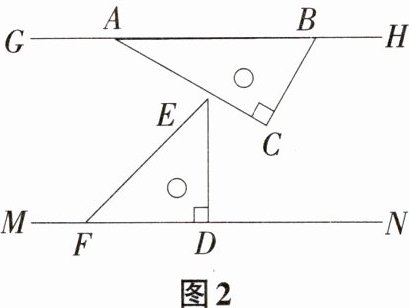
图1 图2
如图,一副三角尺,其中∠EDF=∠ACB=90°,∠E =45°,∠A=30°。
(1)若这副三角尺如图1所示摆放,EF//CD,求∠CDF的度数;
(2)将一副三角尺如图2所示摆放,直线GH//MN,保持三角尺ABC不动,现将三角尺DEF绕点D以每秒3°的速度顺时针旋转,设旋转时间为t s,且0≤t≤60,求当边BC与三角尺DEF的一条直角边(边DE,DF)平行时,所有满足条件的t的值。


图1 图2
答案:
解:
(1)因为EF//CD,∠E = 45°,所以∠CDE = ∠E = 45°, 所以∠CDF = ∠CDE + ∠EDF = 45° + 90° = 135°。
(2)①当BC//DE时,如图,延长AC交MN于点P,延长BC交MN于点Q。 因为BC//DE,所以∠PDE = ∠PQB。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠APD = ∠BAC = 30°,∠PQB = ∠ABC = 60°,
所以∠PDE = 60°,所以∠FDM = 180° - ∠EDF - ∠PDE = 30°。
由题意得∠FDM = (3t)°,所以3t = 30,解得t = 10。
②当BC//DF时,如图,延长BC交MN于点T。
因为BC//DE,所以∠PDE = ∠PQB。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠APD = ∠BAC = 30°,∠PQB = ∠ABC = 60°,
所以∠PDE = 60°,所以∠FDM = 180° - ∠EDF - ∠PDE = 30°。
由题意得∠FDM = (3t)°,所以3t = 30,解得t = 10。
②当BC//DF时,如图,延长BC交MN于点T。 因为BC//DF,所以∠FDN = ∠BTN。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠BTN = ∠ABC = 60°,所以∠FDN = 60°,
所以∠FDM = 180° - ∠FDN = 120°。
由题意得∠FDM = (3t)°,所以3t = 120,解得t = 40。
综上所述,所有满足条件的t的值为10或40。
因为BC//DF,所以∠FDN = ∠BTN。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠BTN = ∠ABC = 60°,所以∠FDN = 60°,
所以∠FDM = 180° - ∠FDN = 120°。
由题意得∠FDM = (3t)°,所以3t = 120,解得t = 40。
综上所述,所有满足条件的t的值为10或40。
解:
(1)因为EF//CD,∠E = 45°,所以∠CDE = ∠E = 45°, 所以∠CDF = ∠CDE + ∠EDF = 45° + 90° = 135°。
(2)①当BC//DE时,如图,延长AC交MN于点P,延长BC交MN于点Q。
 因为BC//DE,所以∠PDE = ∠PQB。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠APD = ∠BAC = 30°,∠PQB = ∠ABC = 60°,
所以∠PDE = 60°,所以∠FDM = 180° - ∠EDF - ∠PDE = 30°。
由题意得∠FDM = (3t)°,所以3t = 30,解得t = 10。
②当BC//DF时,如图,延长BC交MN于点T。
因为BC//DE,所以∠PDE = ∠PQB。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠APD = ∠BAC = 30°,∠PQB = ∠ABC = 60°,
所以∠PDE = 60°,所以∠FDM = 180° - ∠EDF - ∠PDE = 30°。
由题意得∠FDM = (3t)°,所以3t = 30,解得t = 10。
②当BC//DF时,如图,延长BC交MN于点T。 因为BC//DF,所以∠FDN = ∠BTN。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠BTN = ∠ABC = 60°,所以∠FDN = 60°,
所以∠FDM = 180° - ∠FDN = 120°。
由题意得∠FDM = (3t)°,所以3t = 120,解得t = 40。
综上所述,所有满足条件的t的值为10或40。
因为BC//DF,所以∠FDN = ∠BTN。
因为GH//MN,∠EDF = ∠ACB = 90°,∠BAC = 30°,
所以∠BTN = ∠ABC = 60°,所以∠FDN = 60°,
所以∠FDM = 180° - ∠FDN = 120°。
由题意得∠FDM = (3t)°,所以3t = 120,解得t = 40。
综上所述,所有满足条件的t的值为10或40。 查看更多完整答案,请扫码查看


