《2025年初中学霸创新题七年级数学下册北师大版》

12 在△ABC中，已知∠ABC=66°，∠ACB=54°，BE是AC边上的高，CF是AB边上的高，H是BE和CF的交点，则∠EHF的度数是 （ ）

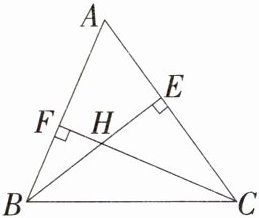
A. 50°
B. 40°
C. 130°
D. 120°

答案： D

13 如图，CD,CE,CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是 （ ）

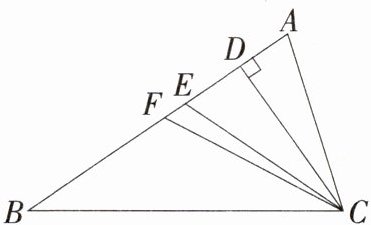
A. AB=2BF
B. ∠ACE=$\frac{1}{2}$∠ACB
C. AE=BE
D. CD⊥BE

答案： C

14（河南许昌魏都区期中）如图，AD,AE分别是△ABC的高和角平分线。若设∠B=α，∠C=β(α＞β)，则用α,β表示∠DAE的关系式为 （ ）

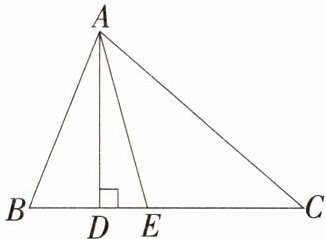
A. 90°-α+β
B. α-β
C. $\frac{\alpha - \beta}{2}$
D. $\frac{\alpha + \beta}{2}$

答案： C

15 新趋势 无图题 在△ABC中，AB=AC，AB边上的高CD与AC夹角为20°，则∠BAC为________。

答案： 70°或110°

16 如图，△ABC的中线AD,BE相交于点F，FH⊥BC，垂足为H。若S△ABC=15，BC=6，则FH长为________。

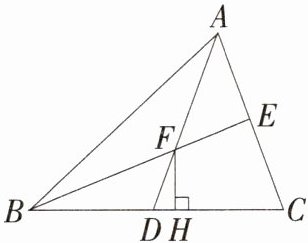
答案： $\frac{5}{3}$

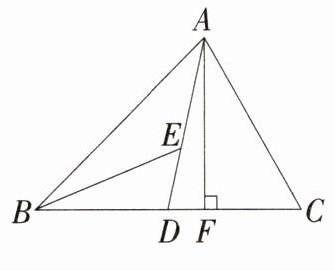
17 如图，在△ABC中，AD,AF分别为△ABC的中线和高，BE为△ABD的一条角平分线。
（1）若∠BED=60°，∠BAD=40°，求∠BAF的大小；
（2）若△ABC的面积为40，BD=5，求AF的长。

答案： 解：
(1)因为∠BED = 60°，所以∠BEA = 180° - ∠BED = 120°。 因为∠BAD = 40°，所以∠ABE = 180° - ∠BEA - ∠BAD = 20°。 因为BE平分∠ABC，所以∠ABC = 2∠ABE = 40°。 因为AF为高，所以∠AFB = 90°， 所以∠BAF = 90° - ∠ABC = 90° - 40° = 50°。
(2)因为AD为中线，所以BC = 2BD = 10。 因为$S_{\triangle ABC}=\frac{1}{2}BC\cdot AF = 40$，所以$AF=\frac{2×40}{10}=8$。

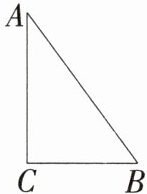
18 新趋势 动点探究题 如图，△ABC中，∠C=90°，AC=4 cm，BC=3 cm，AB=5 cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒2 cm，设运动的时间为t s。
（1）当t=________时，CP把△ABC的周长分成相等的两部分；
（2）当t=________时，CP把△ABC的面积分成相等的两部分；
（3）当t为何值时，△BCP的面积为4 cm²？

答案： 3@@$\frac{13}{4}$@@解：
(1)因为AC = 4 cm，BC = 3 cm，AB = 5 cm， 所以△ABC的周长为4 + 3 + 5 = 12(cm)。 因为CP把△ABC的周长分成相等的两部分，点P的速度为每秒2 cm， 所以$t=\frac{12÷2}{2}=\frac{6}{2}=3$。
(2)当CP把△ABC的面积分成相等的两部分时，点P为AB的中点，所以点P运动的路程为$4+\frac{5}{2}=\frac{13}{2}$(cm)， 所以$t=\frac{13}{2}÷2=\frac{13}{4}$。
(3)当点P在AC上时，因为△BCP的面积为4 cm²， 所以$\frac{1}{2}PC\cdot BC = 4$，即$\frac{1}{2}×2t×3 = 4$，解得$t=\frac{4}{3}$。 当点P在AB上时，△BCP的BP边上的高为$\frac{AC\cdot BC}{AB}=\frac{12}{5}$(cm)。 因为△BCP的面积为4 cm²，所以$BP=\frac{4×2}{\frac{12}{5}}=\frac{10}{3}$(cm)， 所以$AP = 5 - \frac{10}{3}=\frac{5}{3}$(cm)， 所以点P运动的路程为$4+\frac{5}{3}=\frac{17}{3}$(cm)， 所以$t=\frac{17}{3}÷2=\frac{17}{6}$。 综上所述，当t为$\frac{4}{3}$或$\frac{17}{6}$时，△BCP的面积为4 cm²。