《2025年初中学霸创新题七年级数学下册北师大版》

1 如图，一个可以自由转动的转盘，被分成了5个相同的扇形，5个扇形分别标有数字“1”“2”“3”“5”“8”，任意转动转盘1次，指针指向偶数（指针恰好停留在分界线上，则重新转一次）的概率为________。

答案： $\frac{2}{5}$

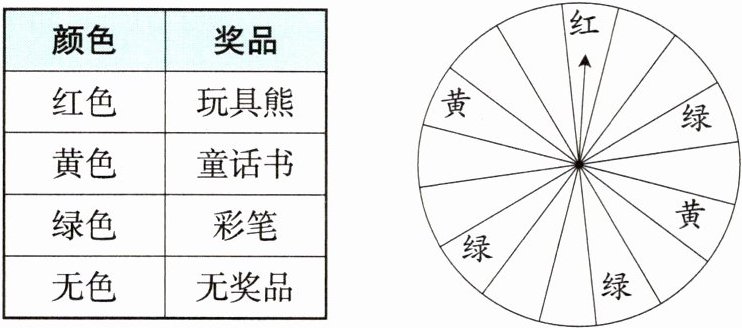
2 [教材P75引例] “六一”儿童节期间，某商厦为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会。如果转盘停止后，指针正好对准哪个区域，顾客就可以获得相应的奖品。
小明和妈妈购买了125元的商品，请你分析计算：
(1)小明获得奖品的概率是多少？
(2)小明获得童话书的概率是多少？

答案： 解：
(1)因为转盘被平均分成16份，其中能获得奖品的部分占6份，所以$P(小明获得奖品)=\frac{6}{16}=\frac{3}{8}$。
(2)因为转盘被平均分成16份，其中黄色部分占2份，所以$P(小明获得童话书)=\frac{2}{16}=\frac{1}{8}$。

3 新情境 生产生活 某路口南北方向红绿灯的设置时间为：红灯57 s，绿灯60 s，黄灯3 s，小明的爸爸由北往南开车随机地行驶到该路口。
(1)他遇到红灯、绿灯、黄灯的概率各是多少？
(2)汽车行驶到路口时，绿灯亮时才能通过，如果遇到黄灯亮或红灯亮时必须在路口外停车等候。问小明的爸爸开车随机到该路口，按照交通信号灯停车等候的概率是多少？

答案： 解：
(1)$P(遇到红灯)=\frac{57}{57 + 60 + 3}=\frac{19}{40}$， $P(遇到绿灯)=\frac{60}{57 + 60 + 3}=\frac{1}{2}$， $P(遇到黄灯)=\frac{3}{57 + 60 + 3}=\frac{1}{40}$。
(2)$P(停车等候)=\frac{57 + 3}{57 + 60 + 3}=\frac{1}{2}$。

4 现要设计一个转盘游戏，使得随机转动转盘一次，指针落在阴影部分的概率为$\frac{1}{6}$，则下列被等分的转盘中符合要求的是 ( )

答案： C

5 如图，把一个圆形转盘按1∶2∶3∶4的比例分成A，B，C，D四个扇形区域，自由转动转盘，停止后指针落在B区域的概率为 ( )


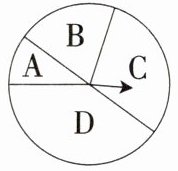
A. $\frac{3}{5}$
B. $\frac{2}{5}$
C. $\frac{1}{5}$
D. $\frac{1}{10}$

答案： C

6 某商场的打折活动规定：凡在本商场购物，可转动转盘一次，并根据所转结果付账。
(1)分别求出打九折、打八折的概率；
(2)求不打折的概率；
(3)小红和小明分别购买了价值200元的商品，活动后一共付钱360元，求他俩获得优惠的情况。

答案： 解：
(1)$P(打九折)=\frac{90^{\circ}}{360^{\circ}}=\frac{1}{4}$；$P(打八折)=\frac{60^{\circ}}{360^{\circ}}=\frac{1}{6}$。
(2)$P(不打折)=\frac{360^{\circ}-90^{\circ}-60^{\circ}}{360^{\circ}}=\frac{7}{12}$。
(3)他俩获得优惠的情况如下： ①一个不打折，一个打八折；②都打九折。