第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
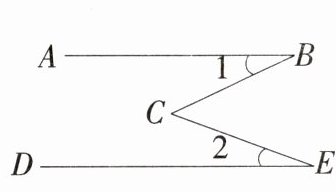
典例1 如图,已知AB//DE,∠1=25°,∠C=45°,则∠2的度数为 ( )
A. 70°
B. 50°
C. 20°
D. 35°
A. 70°
B. 50°
C. 20°
D. 35°

答案:
C
1 新趋势 规律探究题 如图,已知AB//CD,CE,BE的交点为点E,现进行如下操作:
第一次操作:分别作∠ABE和∠DCE的平分线,交点为点E₁;
第二次操作:分别作∠ABE₁和∠DCE₁的平分线,交点为点E₂;
第三次操作:分别作∠ABE₂和∠DCE₂的平分线,交点为点E₃;
……
第n次操作:分别作∠ABEₙ₋₁和∠DCEₙ₋₁的平分线,交点为点Eₙ。
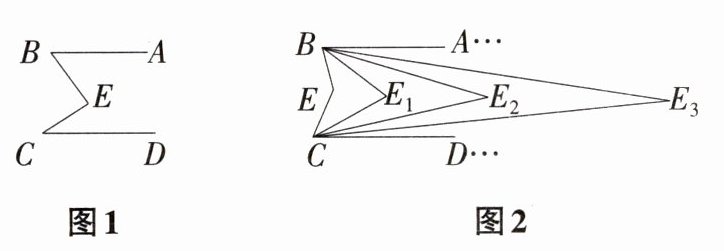
(1)如图1,试说明:∠BEC=∠ABE+∠DCE;
(2)如图2,试说明:∠BE₂C=¼∠BEC;
(3)猜想:若∠BEC=α,那么∠BEₙC的度数为多少?(直接写出结论)
第一次操作:分别作∠ABE和∠DCE的平分线,交点为点E₁;
第二次操作:分别作∠ABE₁和∠DCE₁的平分线,交点为点E₂;
第三次操作:分别作∠ABE₂和∠DCE₂的平分线,交点为点E₃;
……
第n次操作:分别作∠ABEₙ₋₁和∠DCEₙ₋₁的平分线,交点为点Eₙ。

(1)如图1,试说明:∠BEC=∠ABE+∠DCE;
(2)如图2,试说明:∠BE₂C=¼∠BEC;
(3)猜想:若∠BEC=α,那么∠BEₙC的度数为多少?(直接写出结论)
答案:
解:
(1)如图,过点E作EF//AB。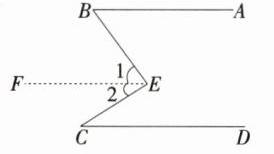
因为AB//CD,所以AB//EF//CD, 所以∠B = ∠1,∠C = ∠2, 所以∠BEC = ∠1 + ∠2 = ∠ABE + ∠DCE。
(2)因为∠ABE和∠DCE的平分线交点为点E₁, 所以由
(1)可得,∠BE₁C = ∠ABE₁ + ∠DCE₁ = $\frac{1}{2}$∠ABE + $\frac{1}{2}$∠DCE = $\frac{1}{2}$(∠ABE + ∠DCE) = $\frac{1}{2}$∠BEC。 因为∠ABE₁和∠DCE₁的平分线交点为点E₂, 所以由
(1)可得,∠BE₂C = ∠ABE₂ + ∠DCE₂ = $\frac{1}{2}$∠ABE₁ + $\frac{1}{2}$∠DCE₁ = $\frac{1}{2}$(∠ABE₁ + ∠DCE₁) = $\frac{1}{2}$∠BE₁C = $\frac{1}{4}$∠BEC。
(3)由
(2)知∠BE₂C = $\frac{1}{4}$∠BEC。 因为∠ABE₂和∠DCE₂的平分线交点为点E₃, 所以∠BE₃C = ∠ABE₃ + ∠DCE₃ = $\frac{1}{2}$∠ABE₂ + $\frac{1}{2}$∠DCE₂ = $\frac{1}{2}$(∠ABE₂ + ∠DCE₂) = $\frac{1}{2}$∠BE₂C = $\frac{1}{8}$∠BEC = $\frac{1}{2^{3}}$∠BEC;…; 以此类推,∠BEₙC = $\frac{1}{2^{n}}$∠BEC。 所以当∠BEC = α时,∠BEₙC = $\frac{\alpha}{2^{n}}$。
解:
(1)如图,过点E作EF//AB。

因为AB//CD,所以AB//EF//CD, 所以∠B = ∠1,∠C = ∠2, 所以∠BEC = ∠1 + ∠2 = ∠ABE + ∠DCE。
(2)因为∠ABE和∠DCE的平分线交点为点E₁, 所以由
(1)可得,∠BE₁C = ∠ABE₁ + ∠DCE₁ = $\frac{1}{2}$∠ABE + $\frac{1}{2}$∠DCE = $\frac{1}{2}$(∠ABE + ∠DCE) = $\frac{1}{2}$∠BEC。 因为∠ABE₁和∠DCE₁的平分线交点为点E₂, 所以由
(1)可得,∠BE₂C = ∠ABE₂ + ∠DCE₂ = $\frac{1}{2}$∠ABE₁ + $\frac{1}{2}$∠DCE₁ = $\frac{1}{2}$(∠ABE₁ + ∠DCE₁) = $\frac{1}{2}$∠BE₁C = $\frac{1}{4}$∠BEC。
(3)由
(2)知∠BE₂C = $\frac{1}{4}$∠BEC。 因为∠ABE₂和∠DCE₂的平分线交点为点E₃, 所以∠BE₃C = ∠ABE₃ + ∠DCE₃ = $\frac{1}{2}$∠ABE₂ + $\frac{1}{2}$∠DCE₂ = $\frac{1}{2}$(∠ABE₂ + ∠DCE₂) = $\frac{1}{2}$∠BE₂C = $\frac{1}{8}$∠BEC = $\frac{1}{2^{3}}$∠BEC;…; 以此类推,∠BEₙC = $\frac{1}{2^{n}}$∠BEC。 所以当∠BEC = α时,∠BEₙC = $\frac{\alpha}{2^{n}}$。
典例2 如图,AB//CD,若∠E=55°,则∠B+∠D= ( )
A. 125°
B. 180°
C. 250°
D. 305°

A. 125°
B. 180°
C. 250°
D. 305°

答案:
D
2 新趋势 规律探究题 (1)如图1,MA₁//NA₂,则∠A₁+∠A₂=________;
如图2,MA₁//NA₃,则∠A₁+∠A₂+∠A₃=________;


如图3,MA₁//NA₄,则∠A₁+∠A₂+∠A₃+∠A₄=________;
如图4,MA₁//NA₅,则∠A₁+∠A₂+∠A₃+∠A₄+∠A₅=________;
(2)如图5,MA₁//NAₙ,则∠A₁+∠A₂+∠A₃+⋯+∠Aₙ=________。
如图2,MA₁//NA₃,则∠A₁+∠A₂+∠A₃=________;


如图3,MA₁//NA₄,则∠A₁+∠A₂+∠A₃+∠A₄=________;
如图4,MA₁//NA₅,则∠A₁+∠A₂+∠A₃+∠A₄+∠A₅=________;
(2)如图5,MA₁//NAₙ,则∠A₁+∠A₂+∠A₃+⋯+∠Aₙ=________。
答案:
180°@@360°@@540°@@720°@@(n - 1)180°
查看更多完整答案,请扫码查看


