《2025年初中学霸创新题七年级数学下册北师大版》

13（易错题）下列算式：
①$3a^{3}\cdot(2a^{2})^{2}=12a^{12}$；②$(2\times10^{3})\times(\frac{1}{2}\times10^{3})=10^{6}$；
③$-3xy\cdot(-2xyz)^{2}=12x^{3}y^{3}z^{2}$；④$4x^{3}\cdot5x^{4}=9x^{12}$。
其中，运算正确的个数是 （ ）
A. 0
B. 1
C. 2
D. 3

答案： B

14 如果单项式$-3m^{6 - 2n}n^{2a + b}$与$mn^{18}$是同类项，那么这两个单项式的积是 （ ）
A. $-3m^{2}n^{36}$
B. $-3m^{6}n^{16}$
C. $-3m^{3}n^{8}$
D. $-9m^{6}n^{16}$

答案： A

15 若单项式$-8x^{a}y$和$\frac{1}{4}x^{2}y^{b}$的积为$-2x^{5}y^{6}$，则$ab$的值为 （ ）
A. 2
B. 30
C. -15
D. 15

答案： D

16 计算：$-10(-a^{3}b^{2}c)^{2}\cdot\frac{1}{5}a\cdot(bc)^{3}-(2abc)^{3}\cdot(-a^{2}b^{2}c)^{2}=$________。

答案： -10a⁷b²c⁵

17 若$(2xy^{2})^{3}\cdot\frac{1}{4}(x^{m}y^{n})^{2}=2x^{7}y^{8}$，则$m=$________，$n=$________。

答案： 2@@1

18 

答案： -36m⁶n³

19 有理数$x$，$y$满足条件$|2x + 4|+(x + 3y + 5)^{2}=0$，求$(-2xy)^{2}\cdot(-y^{2})\cdot6xy^{2}$的值。

答案： 192

20 新考法 如图，将一块棱长分别为$2a$，$a$，$a$的长方体和一块棱长为$a$的正方体组合在一起，再沿线段$AB$竖直将其切开得到一个阴影三棱柱，求余下几何体的体积。

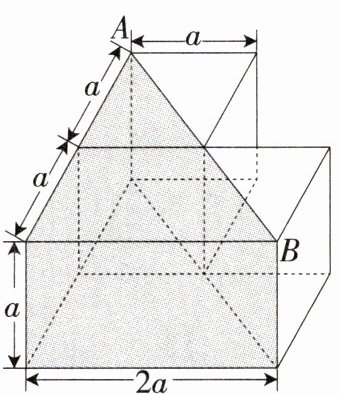
答案： a³

21（湖南衡阳蒸湘区校级期中）若$[-3(x + y)^{m}(x - y)^{2n}]^{2}\cdot[-(x + y)^{2}]=-9(x + y)^{10}(x - y)^{12 - n}$，求$m$，$n$的值。

答案： 4@@12/5

22 新趋势 探究性问题 若$1 + 2 + 3+\cdots + n = m$，且$ab = 1$，$m$为正整数，求$(ab^{n})\cdot(a^{2}b^{n - 1})\cdots(a^{n - 1}b^{2})\cdot(a^{n}b)$的值。

答案： 1