第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
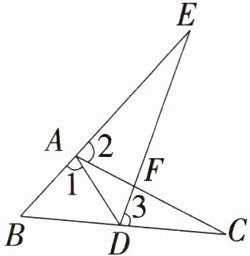
11 如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有 ( )
A. △ABD≌△AFD
B. △AFE≌△ADC
C. △AEF≌△ACB
D. △ABC≌△ADE

A. △ABD≌△AFD
B. △AFE≌△ADC
C. △AEF≌△ACB
D. △ABC≌△ADE
答案:
D
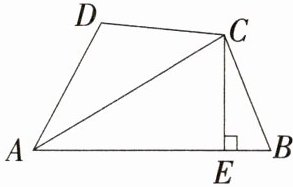
12 (湖南长沙阶段练习)如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AB于点E,AD=6 cm,AB=10 cm,则BE的长度为 ( )
A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm

A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm
答案:
D
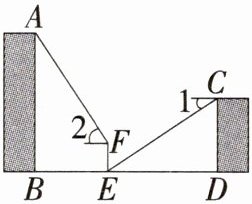
13 新情境 生产生活 如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1 m,BE=CD=20 m,BD=58 m,则单元楼AB的高为 m。

答案:
39
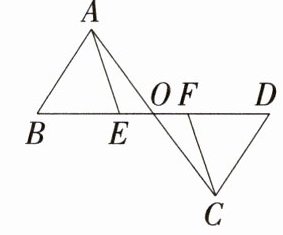
14 已知,如图,E,F在BD上,且AB=CD,BF=DE,AE=CF,试说明:AC与BD互相平分。

答案:
解:因为$BF = DE$,所以$BF - EF = DE - EF$,即$BE = DF$。
在$\triangle ABE$和$\triangle CDF$中,因为$AB = CD$,$BE = DF$,$AE = CF$,所以$\triangle ABE\cong\triangle CDF$,所以$\angle B=\angle D$。
在$\triangle ABO$和$\triangle CDO$中,因为$\angle B=\angle D$,$\angle AOB=\angle COD$,$AB = CD$,所以$\triangle ABO\cong\triangle CDO$,所以$AO = CO$,$BO = DO$,即$AC$与$BD$互相平分。
15 新趋势 探究性问题 已知:△ABC中,∠ACB=90°,AC=CB,D为直线BC上一动点,连接AD,在直线AC右侧作AE⊥AD,且AE=AD。
(1)如图1,当点D在线段BC上时,过点E作EF⊥AC于F,试说明:△ACD≌△EFA;
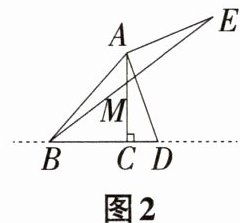
(2)如图2,当点D在线段BC的延长线上时,连接BE交直线AC于点M,试探究BM与EM的数量关系,并说明理由;
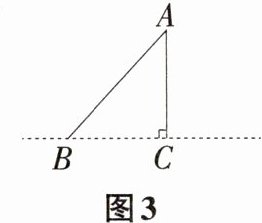
(3)当点D在射线CB上时,连接BE交直线AC于点M,若AC=4CM,请直接写出\frac{S_{\triangle ADB}}{S_{\triangle AEM}}的值。
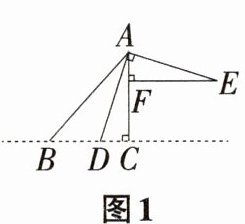
(1)如图1,当点D在线段BC上时,过点E作EF⊥AC于F,试说明:△ACD≌△EFA;
(2)如图2,当点D在线段BC的延长线上时,连接BE交直线AC于点M,试探究BM与EM的数量关系,并说明理由;
(3)当点D在射线CB上时,连接BE交直线AC于点M,若AC=4CM,请直接写出\frac{S_{\triangle ADB}}{S_{\triangle AEM}}的值。



答案:
解:
(1)因为$AE\perp AD$,$EF\perp AC$,$\angle ACB = 90^{\circ}$,所以$\angle AFE=\angle ACB=\angle DAE = 90^{\circ}$,所以$\angle AEF=\angle DAC = 90^{\circ}-\angle EAF$,在$\triangle AEF$和$\triangle DAC$中,$\angle AFE=\angle ACB$,$\angle AEF=\angle DAC$,$AE = DA$,所以$\triangle AEF\cong\triangle DAC$。
(2)$BM = EM$。理由:如图2,作$EF\perp CM$交$CM$的延长线于点$F$, 因为$\angle F = 90^{\circ}$,$\angle ACD = 180^{\circ}-\angle ACB = 90^{\circ}$,$\angle DAE = 90^{\circ}$,所以$\angle F=\angle ACD=\angle MCB$,$\angle FAE=\angle CDA = 90^{\circ}-\angle CAD$,在$\triangle FAE$和$\triangle CDA$中,因为$\angle F=\angle ACD$,$\angle FAE=\angle CDA$,$AE = DA$,所以$\triangle FAE\cong\triangle CDA$,所以$EF = AC = BC$。
在$\triangle BMC$和$\triangle EMF$中,因为对顶角相等,$\angle MCB=\angle F$,$\angle BMC=\angle EMF$,$BC = EF$,所以$\triangle BMC\cong\triangle EMF$,所以$BM = EM$。
因为$\angle F = 90^{\circ}$,$\angle ACD = 180^{\circ}-\angle ACB = 90^{\circ}$,$\angle DAE = 90^{\circ}$,所以$\angle F=\angle ACD=\angle MCB$,$\angle FAE=\angle CDA = 90^{\circ}-\angle CAD$,在$\triangle FAE$和$\triangle CDA$中,因为$\angle F=\angle ACD$,$\angle FAE=\angle CDA$,$AE = DA$,所以$\triangle FAE\cong\triangle CDA$,所以$EF = AC = BC$。
在$\triangle BMC$和$\triangle EMF$中,因为对顶角相等,$\angle MCB=\angle F$,$\angle BMC=\angle EMF$,$BC = EF$,所以$\triangle BMC\cong\triangle EMF$,所以$BM = EM$。
(3)$\frac{2}{5}$或$\frac{2}{3}$。 如图3,当点$D$在$CB$的延长线上时,作$EF\perp AM$交$AM$的延长线于点$F$,则$\angle F=\angle ACD = 90^{\circ}$。 因为$\angle DAE = 90^{\circ}$,所以$\angle FAE=\angle D = 90^{\circ}-\angle DAC$。
在$\triangle AFE$和$\triangle DCA$中,$\angle F=\angle ACD$,$\angle FAE=\angle D$,$AE = DA$,所以$\triangle AFE\cong\triangle DCA$,所以$AF = DC$,$EF = AC = BC$,所以$AF - AC = DC - BC$,所以$CF = DB$。
因为$\angle BCM = 180^{\circ}-\angle ACB = 90^{\circ}$,所以$\angle F=\angle BCM$,在$\triangle EFM$和$\triangle BCM$中,$\angle F=\angle BCM$,$\angle EMF=\angle BMC$,$EF = BC$,所以$\triangle EFM\cong\triangle BCM$,所以$FM = CM$。
设$FM = CM = m$,则$DB = CF = 2m$。
因为$AC = 4CM$,所以$AC = 4m$,所以$AM = 5m$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2m\cdot AC=m\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times5m\cdot AC=\frac{5}{2}m\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{m\cdot AC}{\frac{5}{2}m\cdot AC}=\frac{2}{5}$,所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$。
如图4,当点$D$在线段$BC$上时,设$CM = FM = n$,则$BD = CF = 2n$。
因为$\angle DAE = 90^{\circ}$,所以$\angle FAE=\angle D = 90^{\circ}-\angle DAC$。
在$\triangle AFE$和$\triangle DCA$中,$\angle F=\angle ACD$,$\angle FAE=\angle D$,$AE = DA$,所以$\triangle AFE\cong\triangle DCA$,所以$AF = DC$,$EF = AC = BC$,所以$AF - AC = DC - BC$,所以$CF = DB$。
因为$\angle BCM = 180^{\circ}-\angle ACB = 90^{\circ}$,所以$\angle F=\angle BCM$,在$\triangle EFM$和$\triangle BCM$中,$\angle F=\angle BCM$,$\angle EMF=\angle BMC$,$EF = BC$,所以$\triangle EFM\cong\triangle BCM$,所以$FM = CM$。
设$FM = CM = m$,则$DB = CF = 2m$。
因为$AC = 4CM$,所以$AC = 4m$,所以$AM = 5m$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2m\cdot AC=m\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times5m\cdot AC=\frac{5}{2}m\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{m\cdot AC}{\frac{5}{2}m\cdot AC}=\frac{2}{5}$,所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$。
如图4,当点$D$在线段$BC$上时,设$CM = FM = n$,则$BD = CF = 2n$。 因为$AC = 4CM$,所以$AC = 4n$,所以$AM = 3n$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2n\cdot AC=n\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times3n\cdot AC=\frac{3}{2}n\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{n\cdot AC}{\frac{3}{2}n\cdot AC}=\frac{2}{3}$。
综上所述,$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$或$\frac{2}{3}$。
**核心素养**:本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键。体现了核心素养中的几何直观和推理能力。
因为$AC = 4CM$,所以$AC = 4n$,所以$AM = 3n$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2n\cdot AC=n\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times3n\cdot AC=\frac{3}{2}n\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{n\cdot AC}{\frac{3}{2}n\cdot AC}=\frac{2}{3}$。
综上所述,$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$或$\frac{2}{3}$。
**核心素养**:本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键。体现了核心素养中的几何直观和推理能力。
解:
(1)因为$AE\perp AD$,$EF\perp AC$,$\angle ACB = 90^{\circ}$,所以$\angle AFE=\angle ACB=\angle DAE = 90^{\circ}$,所以$\angle AEF=\angle DAC = 90^{\circ}-\angle EAF$,在$\triangle AEF$和$\triangle DAC$中,$\angle AFE=\angle ACB$,$\angle AEF=\angle DAC$,$AE = DA$,所以$\triangle AEF\cong\triangle DAC$。
(2)$BM = EM$。理由:如图2,作$EF\perp CM$交$CM$的延长线于点$F$,
 因为$\angle F = 90^{\circ}$,$\angle ACD = 180^{\circ}-\angle ACB = 90^{\circ}$,$\angle DAE = 90^{\circ}$,所以$\angle F=\angle ACD=\angle MCB$,$\angle FAE=\angle CDA = 90^{\circ}-\angle CAD$,在$\triangle FAE$和$\triangle CDA$中,因为$\angle F=\angle ACD$,$\angle FAE=\angle CDA$,$AE = DA$,所以$\triangle FAE\cong\triangle CDA$,所以$EF = AC = BC$。
在$\triangle BMC$和$\triangle EMF$中,因为对顶角相等,$\angle MCB=\angle F$,$\angle BMC=\angle EMF$,$BC = EF$,所以$\triangle BMC\cong\triangle EMF$,所以$BM = EM$。
因为$\angle F = 90^{\circ}$,$\angle ACD = 180^{\circ}-\angle ACB = 90^{\circ}$,$\angle DAE = 90^{\circ}$,所以$\angle F=\angle ACD=\angle MCB$,$\angle FAE=\angle CDA = 90^{\circ}-\angle CAD$,在$\triangle FAE$和$\triangle CDA$中,因为$\angle F=\angle ACD$,$\angle FAE=\angle CDA$,$AE = DA$,所以$\triangle FAE\cong\triangle CDA$,所以$EF = AC = BC$。
在$\triangle BMC$和$\triangle EMF$中,因为对顶角相等,$\angle MCB=\angle F$,$\angle BMC=\angle EMF$,$BC = EF$,所以$\triangle BMC\cong\triangle EMF$,所以$BM = EM$。
(3)$\frac{2}{5}$或$\frac{2}{3}$。 如图3,当点$D$在$CB$的延长线上时,作$EF\perp AM$交$AM$的延长线于点$F$,则$\angle F=\angle ACD = 90^{\circ}$。
 因为$\angle DAE = 90^{\circ}$,所以$\angle FAE=\angle D = 90^{\circ}-\angle DAC$。
在$\triangle AFE$和$\triangle DCA$中,$\angle F=\angle ACD$,$\angle FAE=\angle D$,$AE = DA$,所以$\triangle AFE\cong\triangle DCA$,所以$AF = DC$,$EF = AC = BC$,所以$AF - AC = DC - BC$,所以$CF = DB$。
因为$\angle BCM = 180^{\circ}-\angle ACB = 90^{\circ}$,所以$\angle F=\angle BCM$,在$\triangle EFM$和$\triangle BCM$中,$\angle F=\angle BCM$,$\angle EMF=\angle BMC$,$EF = BC$,所以$\triangle EFM\cong\triangle BCM$,所以$FM = CM$。
设$FM = CM = m$,则$DB = CF = 2m$。
因为$AC = 4CM$,所以$AC = 4m$,所以$AM = 5m$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2m\cdot AC=m\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times5m\cdot AC=\frac{5}{2}m\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{m\cdot AC}{\frac{5}{2}m\cdot AC}=\frac{2}{5}$,所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$。
如图4,当点$D$在线段$BC$上时,设$CM = FM = n$,则$BD = CF = 2n$。
因为$\angle DAE = 90^{\circ}$,所以$\angle FAE=\angle D = 90^{\circ}-\angle DAC$。
在$\triangle AFE$和$\triangle DCA$中,$\angle F=\angle ACD$,$\angle FAE=\angle D$,$AE = DA$,所以$\triangle AFE\cong\triangle DCA$,所以$AF = DC$,$EF = AC = BC$,所以$AF - AC = DC - BC$,所以$CF = DB$。
因为$\angle BCM = 180^{\circ}-\angle ACB = 90^{\circ}$,所以$\angle F=\angle BCM$,在$\triangle EFM$和$\triangle BCM$中,$\angle F=\angle BCM$,$\angle EMF=\angle BMC$,$EF = BC$,所以$\triangle EFM\cong\triangle BCM$,所以$FM = CM$。
设$FM = CM = m$,则$DB = CF = 2m$。
因为$AC = 4CM$,所以$AC = 4m$,所以$AM = 5m$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2m\cdot AC=m\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times5m\cdot AC=\frac{5}{2}m\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{m\cdot AC}{\frac{5}{2}m\cdot AC}=\frac{2}{5}$,所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$。
如图4,当点$D$在线段$BC$上时,设$CM = FM = n$,则$BD = CF = 2n$。 因为$AC = 4CM$,所以$AC = 4n$,所以$AM = 3n$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2n\cdot AC=n\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times3n\cdot AC=\frac{3}{2}n\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{n\cdot AC}{\frac{3}{2}n\cdot AC}=\frac{2}{3}$。
综上所述,$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$或$\frac{2}{3}$。
**核心素养**:本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键。体现了核心素养中的几何直观和推理能力。
因为$AC = 4CM$,所以$AC = 4n$,所以$AM = 3n$,
所以$S_{\triangle ADB}=\frac{1}{2}DB\cdot AC=\frac{1}{2}\times2n\cdot AC=n\cdot AC$,
$S_{\triangle AEM}=\frac{1}{2}AM\cdot EF=\frac{1}{2}\times3n\cdot AC=\frac{3}{2}n\cdot AC$,
所以$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}=\frac{n\cdot AC}{\frac{3}{2}n\cdot AC}=\frac{2}{3}$。
综上所述,$\frac{S_{\triangle ADB}}{S_{\triangle AEM}}$的值为$\frac{2}{5}$或$\frac{2}{3}$。
**核心素养**:本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键。体现了核心素养中的几何直观和推理能力。 1 新情境 生产生活 如图是工厂里常用的可用于测量零件内槽宽的工具(卡钳),它由两根等长的钢条AA'和BB'在中点处连接而成,只要测出A'B'长就知道AB的长,用到的原理为全等三角形的哪个判定方法 ( )
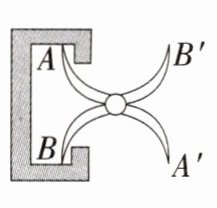
A. SAS B. AAS C. SSS D. ASA

A. SAS B. AAS C. SSS D. ASA
答案:
A
查看更多完整答案,请扫码查看


