第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1(河南洛阳期末)某商家搞营销活动,顾客买商品后抽奖券,中奖概率为0.2。对“中奖概率为0.2”这句话,下列理解正确的是 ( )
A. 抽1张奖券肯定不会中奖
B. 抽100张奖券肯定会中2张奖
C. 抽1张奖券也可能会中奖
D. 抽100张奖券至少中1张奖
A. 抽1张奖券肯定不会中奖
B. 抽100张奖券肯定会中2张奖
C. 抽1张奖券也可能会中奖
D. 抽100张奖券至少中1张奖
答案:
C
2 掷一枚质地均匀的骰子,骰子停止后,在下列四个选项中,概率最大的是 ( )
A. 点数小于4
B. 点数大于4
C. 点数大于5
D. 点数小于5
A. 点数小于4
B. 点数大于4
C. 点数大于5
D. 点数小于5
答案:
D
3 在一个不透明的纸盒中放入颜色分别为白色、红色、绿色的小球各1个,每个小球除颜色不同外其他均相同,三人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出白球者赢,则这个游戏中先摸者赢的概率________后摸者赢的概率。(填“>”“<”或“=”)
答案:
=
4 关于频率和概率的关系,下列说法正确的是 ( )
A. 频率等于概率
B. 当试验次数很大时,频率稳定在概率附近
C. 当试验次数很大时,概率稳定在频率附近
D. 试验得到的频率与概率不可能相等
A. 频率等于概率
B. 当试验次数很大时,频率稳定在概率附近
C. 当试验次数很大时,概率稳定在频率附近
D. 试验得到的频率与概率不可能相等
答案:
B
5 某射击运动员在同一条件下的射击成绩记录如下:
|射击次数|100|200|400|800|1 000|
|----|----|----|----|----|----|
|“射中九环以上”的次数|87|172|336|679|850|
|“射中九环以上”的频率|0.87|0.86|0.84|0.85|0.85|
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是 ( )
A. 0.84
B. 0.85
C. 0.86
D. 0.87
|射击次数|100|200|400|800|1 000|
|----|----|----|----|----|----|
|“射中九环以上”的次数|87|172|336|679|850|
|“射中九环以上”的频率|0.87|0.86|0.84|0.85|0.85|
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是 ( )
A. 0.84
B. 0.85
C. 0.86
D. 0.87
答案:
B
6 在一个不透明的口袋中有红色、黄色和绿色球共80个,它们除颜色外,其余完全相同。在不倒出球的情况下,估计袋中各种颜色球的个数。同学们通过大量的摸球试验后,发现摸到红色球和绿色球的频率分别稳定在20%和40%。由此,推测口袋中黄色球有 ( )
A. 16个
B. 18个
C. 21个
D. 32个
A. 16个
B. 18个
C. 21个
D. 32个
答案:
D
7 新情境 生产生活 某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由此可估计这种树苗移植1 200棵,成活的大约有________棵。
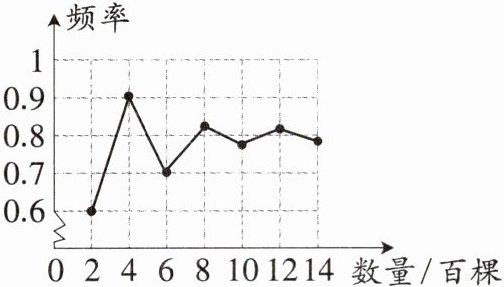

答案:
960
8 [教材P70T1 改编]某市羽毛球厂对生产的羽毛球进行产品质量检查,结果如下:
|抽取球数|100|500|1 000|5 000|
|----|----|----|----|----|
|优等品数|92|455|890|4 500|
|优等品率| | | | |
(1)计算各次检查中的优等品率,并填入上表;
(2)该厂生产的羽毛球为优等品的概率大约是________。
|抽取球数|100|500|1 000|5 000|
|----|----|----|----|----|
|优等品数|92|455|890|4 500|
|优等品率| | | | |
(1)计算各次检查中的优等品率,并填入上表;
(2)该厂生产的羽毛球为优等品的概率大约是________。
答案:
解:
(1) 优等品率分别为92÷100 = 0.92,455÷500 = 0.91,890÷1 000 = 0.89,4 500÷5 000 = 0.9。 填表如下: |抽取球数|100|500|1 000|5 000| |----|----|----|----|----| |优等品数|92|455|890|4 500| |优等品率|0.92|0.91|0.89|0.90|
(2) 0.90 提示:由于试验次数越大,频率越接近概率,故该厂生产的羽毛球为优等品的概率大约是0.90。
(1) 优等品率分别为92÷100 = 0.92,455÷500 = 0.91,890÷1 000 = 0.89,4 500÷5 000 = 0.9。 填表如下: |抽取球数|100|500|1 000|5 000| |----|----|----|----|----| |优等品数|92|455|890|4 500| |优等品率|0.92|0.91|0.89|0.90|
(2) 0.90 提示:由于试验次数越大,频率越接近概率,故该厂生产的羽毛球为优等品的概率大约是0.90。
9 一个口袋中有5个黑球和若干个白球,从口袋中随机摸出一球,记下其颜色,再把它放回摇匀,重复上述过程,共试验100次,其中75次摸到白球,于是可以估计口袋中共有多少个球?
答案:
解:因为试验100次,其中75次摸到白球,
所以估计摸到白球的概率为0.75。
设口袋中共有x个球,则0.75x = x - 5,解得x = 20,
所以估计口袋中共有20个球。
查看更多完整答案,请扫码查看


