《2025年初中学霸创新题七年级数学下册北师大版》

典例1 如图，在△ABC中，∠A = 90°，AB = AC，∠ABC的平分线BD交AC于点D，CE⊥BD，交BD的延长线于点E，若BD = 8，则CE = ________。
学霸说 遇角平分线，可在其两侧构造全等三角形。本题通过延长BA和CE相交于点F，结合已知条件得△BFE≌______，△ACF≌______，得到EF = ______，CF = ______，进而求解。
【答案】

答案：
@4

1 如图，在△ABC中，BP平分∠ABC，AP⊥BP，垂足为P，连接PC，若△ABC的面积为1 cm²，则△PBC的面积为 ( )
A. 0.4 cm²
B. 0.5 cm²
C. 0.6 cm²
D. 0.7 cm²

答案： B

2 如图，在Rt△ABC中，∠ACB = 90°，AC = 3，BC = 4，AB = 5，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE + EF的最小值为 ________。

答案： $\frac{12}{5}$

典例2 △ABC中，AB = 5，AC = 3，AD是△ABC的中线，设AD长为m，则m的取值范围是________。

答案：
@1<m<4

3 (河南郑州中原区期中)如图，在△AEC中，点B，D在EC上，∠E = ∠CAD，点D是BC的中点，若AB平分∠DAE，试说明：AC = BE。

答案：
解：延长AD至F，使DF = AD，连接CF，如图所示。 因为点D是BC的中点，所以BD = DC。 在△ABD和△FCD中， 因为BD = CD，∠ADB = ∠FDC，AD = FD， 所以△ABD≌△FCD，所以∠BAD = ∠CFD，AB = FC。 因为AB平分∠DAE， 所以∠BAD = ∠EAB，所以∠CFD = ∠EAB。 在△FCA和△ABE中， 因为∠CFD = ∠BAE，∠CAD = ∠E，CF = BA， 所以△FCA≌△ABE，所以AC = BE。

4 如图，AB = AE，AB⊥AE，AD = AC，点M为BC的中点，连接AM，DE = 2AM。试说明：AD⊥AC。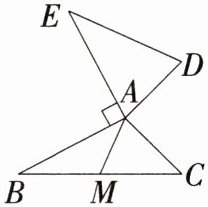

答案：
解：如图，延长AM至N，使MN = AM，连接BN，则AN = 2AM = DE。  因为点M为BC的中点，所以CM = BM。 在△AMC和△NMB中， 因为AM = NM，∠AMC = ∠NMB，CM = BM， 所以△AMC≌△NMB， 所以AC = BN = AD，∠C = ∠NBM，所以AC//BN。 在△EAD和△ABN中，因为AE = BA，AD = BN，ED = AN， 所以△EAD≌△ABN，所以∠EAD = ∠ABN。 因为AC//BN，所以∠CAM = ∠N， 所以∠BAC + ∠EAD = ∠BAM + ∠N + ∠ABN = 180°， 所以∠BAE + ∠DAC = 180°。 又因为AB⊥AE，所以∠BAE = 90°， 所以∠DAC = 90°，即AD⊥AC。