《2025年初中学霸创新题七年级数学下册北师大版》

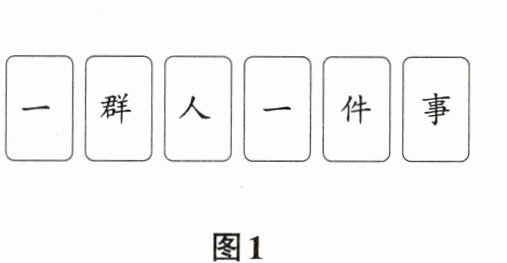
1 如图1，有6张写有汉字的卡片，它们的背面都相同，现将它们背面朝上洗匀后如图2摆放，从中任意翻开一张是汉字“人”的概率是 （ ）
一 群 人 一 件 事
图1 图2

A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{1}{6}$

答案： D

2 新情境 数学文化 只有1和它本身两个因数且大于1的自然数叫作素数，我国数学家陈景润在有关素数的“哥德巴赫猜想”的研究中取得了世界领先的成果。从5,7,11这3个素数中随机抽取一个，则抽到的数是7的概率是 （ ）
A. $\frac{1}{7}$
B. $\frac{1}{5}$
C. $\frac{1}{3}$
D. 1

答案： C

3 [教材P73例题 改编]一个质地均匀的小正方体，六个面分别标有数字1,2,3,4,5,6，掷小正方体后，观察朝上一面的数字出现偶数的概率是 （ ）
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{2}{3}$

答案： A

4 [教材P73随堂练习T2 改编]在同一副扑克牌中抽取2张“方块”，3张“梅花”，1张“红桃”，将这6张牌背面朝上，从中任意抽取1张，是“梅花”的概率为 （ ）
A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$

答案： C

5（浙江宁波中考）一个不透明的袋子里装有5个红球和6个白球，它们除颜色外其余都相同。从袋中任意摸出一个球是红球的概率为________。

答案： $\frac{5}{11}$

6 新趋势 跨学科融合（四川南充中考）老师为帮助学生正确理解物理变化与化学变化，将6种生活现象制成看上去无差别的卡片（如图）。从中随机抽取一张卡片，抽中生活现象是物理变化的概率是________。
冰化成水 物理变化 铁棒生锈 化学变化 酒精燃烧 化学变化
衣服晾干 物理变化 光合作用 化学变化 牛奶变质 化学变化

答案： $\frac{1}{3}$

7 明明家过年时包了50个饺子，其中有4个饺子包有幸运果。明明在饺子中任意挑选一个饺子，正好是包有幸运果饺子的概率是________。

答案： $\frac{2}{25}$

8 甲、乙两人玩“石头、剪刀、布”的游戏。他们在不透明的袋子中放入形状、大小均相同的10张卡片，其中写有“石头”“剪刀”“布”的卡片张数分别为2,3,5。两人各随机摸出一张卡片（先摸者不放回）来比胜负，并约定：“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”，同种卡片不分胜负。
(1)若甲先摸，则他摸到“石头”的概率是多少？
(2)若甲先摸到了“石头”，则乙获胜的概率是多少？

答案： 解：
(1)甲摸到“石头”的概率为$\frac{2}{2 + 3 + 5}=\frac{1}{5}$。
(2)因为甲先摸到了“石头”，又要乙获胜，所以乙必须摸到“布”，所以乙获胜的概率为$\frac{5}{2 + 3 + 5 - 1}=\frac{5}{9}$。