《2025年初中学霸创新题七年级数学下册北师大版》

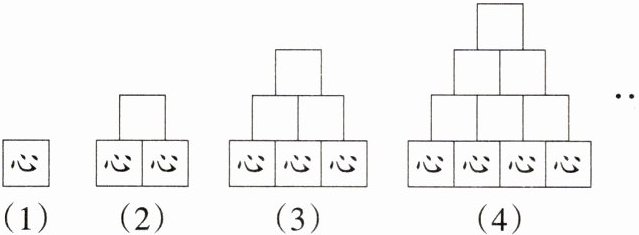
9 新趋势 规律探究题 小明用大小和形状都完全一样的正方体按照一定规律摆放成一组图案（如图所示），每个图案中只在最下面的正方体上写“心”字，寓意“不忘初心”。其中第(1)个图案中有1个正方体，第(2)个图案中有3个正方体，第(3)个图案中有6个正方体，……按照此规律，从第(100)个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是 （ ）
心 心 心 心
(1) (2) (3) (4)

A. $\frac{1}{100}$
B. $\frac{1}{20}$
C. $\frac{1}{101}$
D. $\frac{2}{101}$

答案： D

10 在一个不透明的袋子中装有3个白球和若干个红球，它们除颜色外，大小、质地都相同。从袋子中随机取出一个球，若取得白球的概率是0.3，那么袋中装有红球的个数为________。

答案： 7

11（河南郑州期末）请你举例写出一个事件，使得该事件发生的概率为$\frac{2}{5}$。例如：________________________。

答案： 盒子里有三个白球，两个黑球，取出一个球，取到黑球的概率为$\frac{2}{5}$(答案不唯一)

12（易错题）如图，有一个正十二面体，12个面上分别写有1～12这12个整数，投掷这个正十二面体一次，向上一面的数字是3的倍数或4的倍数的概率是________。

答案： $\frac{1}{2}$

13 新趋势 多模块综合 有5张相同的卡片，卡片正面分别标有-2,|-3|,(-2)^2,-(-\frac{1}{4})^0,(-1)^2，将卡片背面朝上，从中随机抽取1张，则抽取的卡片上的数是正数的概率为________。

答案： $\frac{3}{5}$

14 从背面相同的同一副扑克牌中取出9张红桃，10张黑桃，11张方块。
(1)将取出的这些牌洗匀背面朝上放在桌面上，从中随机抽出一张是红桃的概率；
(2)若先从取出的这些牌中抽掉6张红桃和m张黑桃后，将剩下的牌洗匀背面朝上放在桌面上，从中再随机抽出一张牌，若抽取黑桃的概率为$\frac{1}{3}$，求m的值。

答案： 解：
(1)因为9 + 10 + 11 = 30， 所以从中随机抽出一张牌，共有30种等可能结果，其中出现红桃的有9种结果， 所以从中随机抽出一张是红桃的概率是$\frac{9}{30}=\frac{3}{10}$。
(2)因为9 + 10 + 11 - 6 - m = 24 - m， 所以抽掉6张红桃和m张黑桃后，桌面上共有(24 - m)张牌，其中黑桃有(10 - m)张， 所以从中再随机抽出一张牌，共有(24 - m)种等可能结果，其中出现黑桃的有(10 - m)种结果。 又因为抽取黑桃的概率为$\frac{1}{3}$， 所以$\frac{1}{3}(24 - m)=10 - m$，解得m = 3，所以m的值为3。

15 新趋势 规律探究题 一场数学游戏在两名学生甲、乙之间进行，裁判在黑板上写出正整数2,3,4, …,2 006，然后随意擦去一个数，接下来由乙、甲两人轮流擦去其中一个数（即乙先擦去其中一个数，然后甲再擦去一个数）。如此下去，若最后剩下的两个数为互质数，则判甲胜；否则，判乙胜。按照这种游戏规则，求甲获胜的概率。(用具体数字作答)

答案： 解：获胜的关键，要看裁判擦去的数是奇数还是偶数，注意到2，3，4，…，2 006中有1 003个偶数，1 002个奇数。所以分两种情况： ①若裁判擦去的数是奇数，则乙一定获胜。 乙不管甲擦去什么数，只要有奇数，乙就擦去奇数(没有奇数时才擦去偶数)，这样最后两个数一定都是偶数，它们不为互质数，故乙胜。 ②若裁判擦去的数是偶数2m(m是正整数)，则所剩的2 004个数可配成1 002对，每对中两个数互质：(2，3)，(4，5)，…，(2m - 2，2m - 1)，(2m + 1，2m + 2)，…，(2 005，2 006)。 这样不管乙擦去哪个数，甲都擦去所配对中另一个数，最后剩下的必然是配成一对的两个数，它们互质，故甲胜。 所以甲获胜的概率为$\frac{1 003}{2 005}$。 核心素养 本题考查的是概率公式，利用分类讨论的思想进行解答是解题的关键。体现了核心素养中的推理能力。