《2025年伴你学九年级数学下册苏科版》

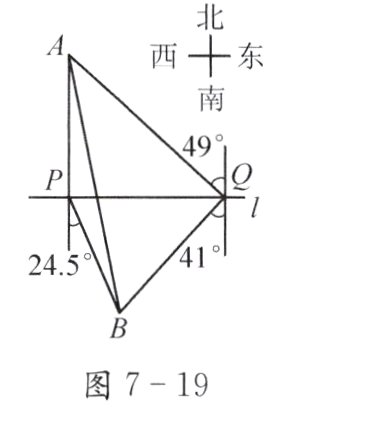
如图7 - 19，自来水厂A和村庄B分别在小河l的两侧，现要在A、B间铺设一条输水管道。为了做好工程预算，需测算出A、B间的距离。一小船在点P处测得自来水厂A在正北方向，村庄B位于南偏东24.5°方向；小船前行1200 m到达点Q处，测得自来水厂A位于北偏西49°方向，村庄B位于南偏西41°方向。
(1) 线段BQ与PQ是否相等？请说明理由。
(2) 求A、B间的距离(参考数据：cos 41°≈0.75)。

答案： （1）$BQ = BP$，可得$\angle PQB = 49^{\circ}$，$\angle QPB = 65.5^{\circ}$，$\angle QBP = 65.5^{\circ}$ （2）$AB = 2000\ m$

(1) 表中n的值为________；该小组选择不同的位置测量三次，再以三次测量计算的旗杆高度的平均数作为结论，这样做的目的是________________。
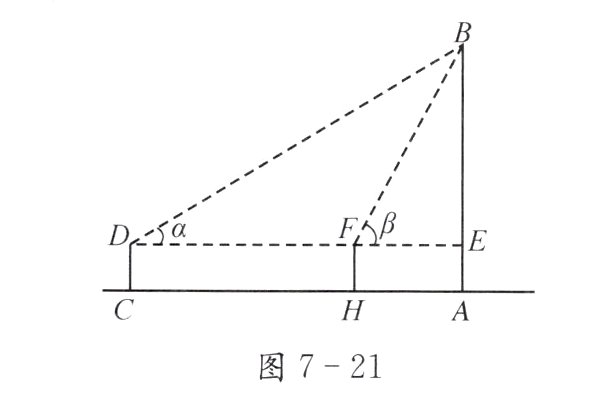
(2) 该测量模型中，若CD = a，AC = b，仰角为α，用含a、b、α的代数式表示旗杆AB的高度为________。
(3) 第二小组方案如下：测量示意图如图7 - 21所示，测角仪的高度为1 m，先在点C处测得旗杆顶端B的仰角α为30°，然后朝旗杆方向前进14 m到达点H处，再次测得旗杆顶端B的仰角β为60°，请你求出旗杆AB的高度(结果保留根号)。

答案： （1）$13.1$；减小误差 （2）$b\tan\alpha + a$ （3）$DC = FH = AE = 1\ m$，$DF = CH = 14\ m$，$\angle DEB = 90^{\circ}$，$\angle BFE = 60^{\circ}$，$\angle BDF = 30^{\circ}$。$\therefore \angle DBF = \angle BFE - \angle BDF = 30^{\circ}$。$\therefore \angle BDF = \angle DBF = 30^{\circ}$。$\therefore FD = FB = 14\ m$。在$Rt\triangle BFE$中，$BE = BF\cdot\sin60^{\circ}=14\times\frac{\sqrt{3}}{2}=7\sqrt{3}(m)$，$\therefore AB = BE + AE=(1 + 7\sqrt{3})m$