《2025年伴你学九年级数学下册苏科版》

4. 求下列各式的值.
(1) 2 sin 30°-cos 45°； (2) sin²45°+tan 30°·sin 60°； (3) sin²30°+cos²30°.

答案： [检测反馈]4.
(1) $1 - \frac{\sqrt{2}}{2}$
(2) 1
(3) 1

5. 求满足下列条件的锐角.
$(1) sin α-\frac{\sqrt{3}}{2}=0；$$ (2) -2cos α+\sqrt{3}=0；$$ (3) tan (α+10°)=\sqrt{3}.$

答案： [检测反馈]5.
(1) 60°
(2) 30°
(3) 50°

6. 已知sin (α-β)=sin α·cos β-cos α·sin β，请利用特殊角的三角函数值计算sin 15°的值.

答案： [检测反馈]6. $\frac{\sqrt{6}-\sqrt{2}}{4}$

1. 如图，以点O为圆心，任意长为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则cos ∠AOB=________.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

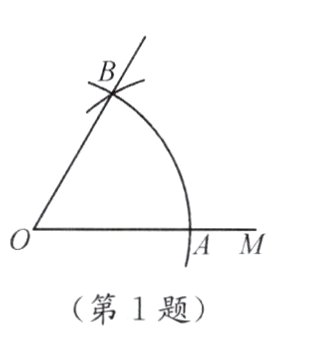
答案： [迁移运用]1. $\frac{1}{2}$

2. 在Rt△ABC中，∠C=90°，AB=2BC. 有下列结论：$① sin A=\frac{\sqrt{3}}{2}；$$② cos B=\frac{1}{2}；$$③ tan A=\frac{\sqrt{3}}{3}；$$④ tan B=\sqrt{3}. $其中，正确的是________(填序号).

答案： [迁移运用]2. ②③④

3. 如图，在距离水面5 m高的岸上有人用绳子拉船靠岸. 开始时绳子与水面的夹角为30°，此人以0.5 m/s的速度收绳. 求8 s后船向岸边移动的距离.

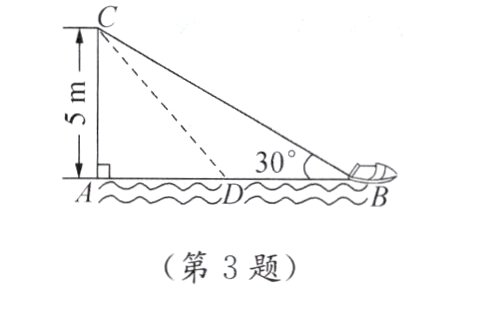
答案： [迁移运用]3. $(5\sqrt{3}-\sqrt{11})\text{ m}$