《2025年伴你学九年级数学下册苏科版》

4. 如图，已知某零件的外径为25 mm，现用一个交叉卡钳(AC = BD，OC = OD)测量零件的内径AB.若OC:OA = 1:2，测得CD = 10 mm，则零件的厚度x = ________mm.
　　　

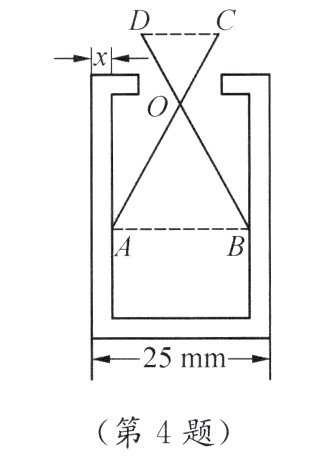
答案： 2.5

5. 如图，△ABC是等边三角形，被一平行于BC的矩形所截，AB被截成三等份，图中阴影部分面积是△ABC面积的________.
　　　

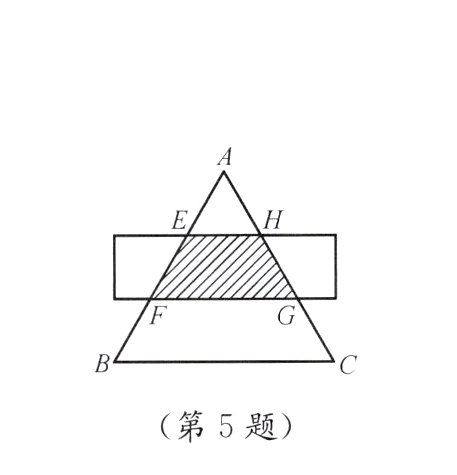
答案： $\frac{1}{3}$

6. 如图，∠ABD = ∠C = 90°，AD = 10，BD = 6.若△ABD与△BCD相似，则CD的长是________.
　　　

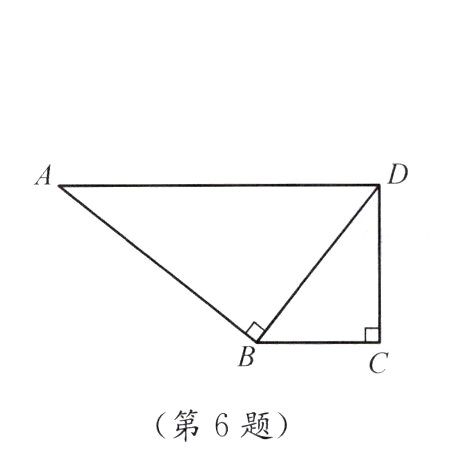
答案： $\frac{18}{5}$或$\frac{24}{5}$

迁移运用
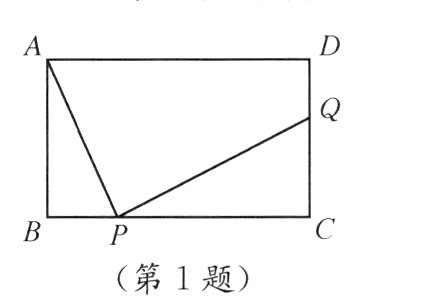
1. 如图，在矩形ABCD中，AB = 9，BC = 15，动点P、Q分别在边BC、CD上.要求添加条件后，提出一个问题并解决. 甲、乙两人的做法如下.
甲：若CQ = 4，则在BC上存在2个点P，使△ABP与△PCQ相似；
乙：若AP⊥PQ，则CQ的最大值为$\frac{25}{4}$.
下列判断中，正确的是(　　　)．
A. 甲对，乙错 B. 甲错，乙对 C. 甲、乙都对 D. 甲、乙都错
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： B

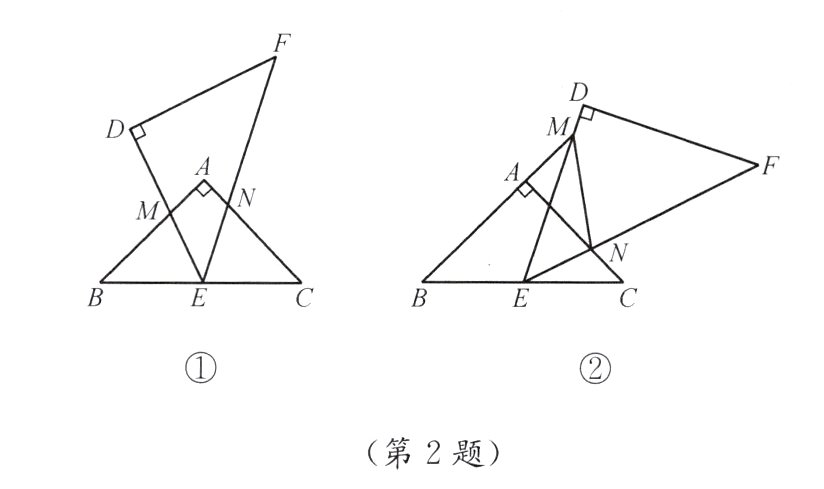
2. 如图，已知△ABC和△DEF是两个等腰直角三角形，∠A = ∠D = 90°，△DEF的顶点E位于△ABC的边BC的中点上.
（1）如图①，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；
（2）如图②，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，除(1)中的一对相似三角形外，能否再找出一对相似三角形(等腰三角形除外)并证明你的结论?
　　　

答案：
(1)由$\angle BEM+\angle NEC = 135^{\circ}$，$\angle BEM+\angle BME = 135^{\circ}$，可得$\angle BME = \angle CEN$，而$\angle B = \angle C$，所以$\triangle BEM\sim\triangle CNE$　
(2) $\triangle BEN\sim\triangle ENM$或$\triangle CNE\sim\triangle ENM$