第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
2. 如图,AD⊥CD,AB = 10,BC = 20,∠A = ∠C = 30°,则AD的长为_______,CD的长为_______.
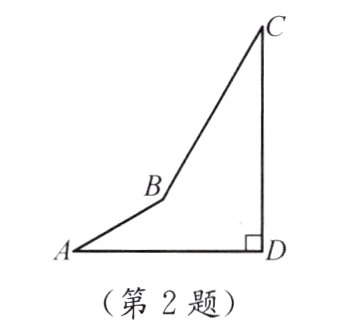

答案:
5√3 + 10 10√3 + 5
3. 如图,两堵墙之间有一架底端在点A的梯子,当它靠在一侧墙上时,梯子的顶端在点B;当它靠在另一侧墙上时,梯子的顶端在点D. 已知∠BAC = 60°,∠DAE = 45°,DE = 3$\sqrt{2}$ m,则点B到地面的距离BC = _______m.
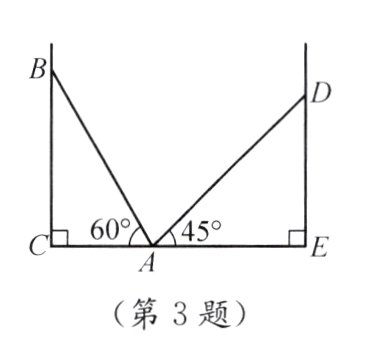

答案:
3√3
4. 如图,在△ABC中,AD是边BC上的高,∠C = 45°,sinB = $\frac{1}{3}$,AD = 1. 求BC的长.
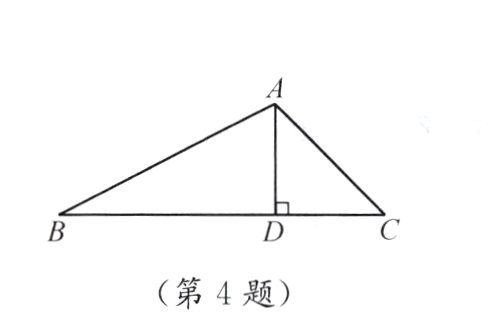

答案:
2√2 + 1
1. 如图,在矩形ABCD中,对角线AC、BD相交于点O,∠BOC = 120°,AB = 2.
(1)求AC、BD的长.
(2)过点O作OE⊥AD,垂足为E,连接BE. 设∠ABE = α,求tanα的值.
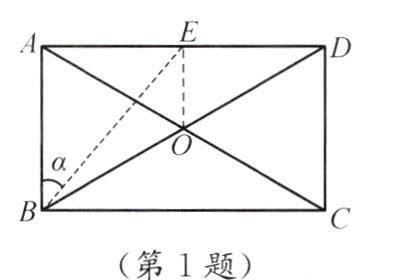
(1)求AC、BD的长.
(2)过点O作OE⊥AD,垂足为E,连接BE. 设∠ABE = α,求tanα的值.

答案:
(1) AC = BD = 4
(2) tanα = √3/2
(1) AC = BD = 4
(2) tanα = √3/2
2. 如图是一座独塔双索结构的斜拉桥,主塔采用倒“Y”形设计,某学习小组利用课余时间测量主塔顶端到桥面的距离,勘测记录如下表:


请利用表中提供的信息,求主塔顶端E到AB的距离(参考数据:sin28°≈0. 47,cos28°≈0. 88,tan28°≈0. 53).


请利用表中提供的信息,求主塔顶端E到AB的距离(参考数据:sin28°≈0. 47,cos28°≈0. 88,tan28°≈0. 53).
答案:
主塔顶端E到AB的距离约为47.7m. 延长EF交AB于点M,
∵EF⊥AB,点A、C分别与点B、D关于直线EF对称,CD = 12m,
∴∠AME = 90°,CM = DM = 1/2CD = 6(m).
∵∠A = 28°,AC = 84m,
∴AM = AC + CM = 90(m).
∴tanA = EM/AM≈0.53.
∴EM≈47.7(m)

主塔顶端E到AB的距离约为47.7m. 延长EF交AB于点M,
∵EF⊥AB,点A、C分别与点B、D关于直线EF对称,CD = 12m,
∴∠AME = 90°,CM = DM = 1/2CD = 6(m).
∵∠A = 28°,AC = 84m,
∴AM = AC + CM = 90(m).
∴tanA = EM/AM≈0.53.
∴EM≈47.7(m)

查看更多完整答案,请扫码查看


