《2025年伴你学九年级数学下册苏科版》

3. 已知点C是线段AB的黄金分割点，AB=10，则线段AC=_______.

答案： $15 - 5\sqrt{5}$或$5\sqrt{5} - 5$

4. 大自然巧夺天工，一片树叶也蕴含着“黄金分割”.如图，P为线段AB的黄金分割点(AP＞PB)，如果线段AB的长度为8 cm，那么AP的长度是_________(精确到0.01 cm).

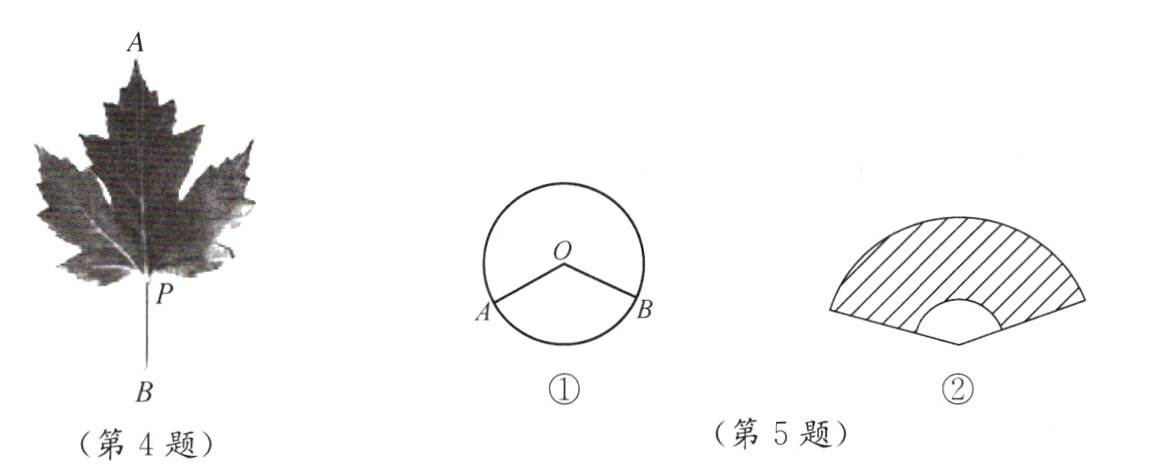
答案： 4.94cm

5. 如图①，折线段AOB将面积为S的⊙O分成两个扇形，大扇形、小扇形的面积分别为S₁、S₂.若$\frac{S_{1}}{S}=\frac{S_{2}}{S_{1}}=0.618$，则称分成的小扇形为“黄金扇形”.生活中的折扇(图②)大致是“黄金扇形”，“黄金扇形”的圆心角约为_______°(精确到0.1°).

答案： 137.5

1. 填空：
(1) 若M是线段AB的黄金分割点，且AB=1，则AM=_______(保留根号).
(2) 若M、N是线段AB上的两个黄金分割点，且AB=1 cm，则MN=_______cm(保留根号).

答案：
(1)$\frac{\sqrt{5} - 1}{2}$或$\frac{3 - \sqrt{5}}{2}$　
(2)$\sqrt{5} - 2$

2. 宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫作黄金矩形.心理测试表明：黄金矩形令人赏心悦目，它给我们以协调匀称的美感.小明在数学活动课中画黄金矩形如图所示，方法归纳如下：
(1) 画正方形ABCD；
(2) 分别取AD、BC的中点M、N，连接MN；
(3) 以点N为圆心，ND长为半径画弧，交BC的延长线于点E；
(4) 过点E作EF⊥AD，交AD的延长线于点F.
请证明矩形DCEF为黄金矩形.

B　　N　　C　　E

答案： 设正方形ABCD的边长为a，可得NE=ND=$\frac{\sqrt{5}}{2}$a,CE=$\frac{\sqrt{5}-1}{2}$a,则$\frac{CE}{CD}$=$\frac{\sqrt{5}-1}{2}$≈0.618