《2025年伴你学九年级数学下册苏科版》

3. 如图，在$\triangle ABC$中，$DE// BC$，$AH\perp BC$，垂足为$H$，$AH$交$DE$于点$G$，$AD∶BD = 1∶2$. 下列结论中，错误的是( ).
A. $\frac{AE}{AC}=\frac{1}{3}$ B. $\frac{AG}{AH}=\frac{1}{3}$ C. $\frac{\triangle ADE的周长}{\triangle ABC的周长}=\frac{1}{3}$ D. $\frac{\triangle ADE的面积}{\triangle ABC的面积}=\frac{1}{3}$
　　　　　　　 　　　

答案： D

4. 如图，在$\triangle ABC$中，点$D、E$分别在$AB、AC$上，$AB = 10\ cm$，$AC = 8\ cm$，$AD = 4\ cm$，$AE = 5\ cm$. 若点$A$到$BC$的距离为6 cm，试求点$A$到$DE$的距离.

答案： 3cm

1. 如图，小明右手握直尺，手臂向前伸直保持直尺与地面垂直，前后移动调整自己的位置，直到看见直尺露出的部分刚好遮住树的主干，这时通过测量眼睛到直尺的距离$AB$、小明到树干的距离$AC$，以及露出的直尺长度$DE$，就可以算得树的高度，这种测量方案主要应用了相似三角形的性质定理：____________________(填写定理内容).
　　　　　　　　　　　　　　　　　　　　　

答案： 相似三角形对应高的比等于相似比

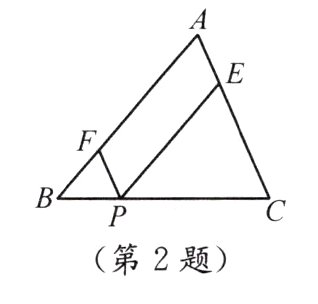
2. 如图，在$\triangle ABC$中，$P$是边$BC$上的任意一点(点$P$与点$B、C$不重合)，$\square AFPE$的顶点$F、E$分别在$AB、AC$上. 已知$BC = 2$，$S_{\triangle ABC}=1$. 设$BP = x$，$\square AFPE$的面积为$y$.
(1) 求$y$与$x$之间的函数表达式.
(2) 上述函数有最大值或最小值吗？若有，求出当$x$取何值时，$y$的值最大或最小. 最大值或最小值是多少？若没有，请说明理由.
　　　

答案：
(1)
∵四边形AFPE是平行四边形，
∴PF//CA，
∴△BFP∽△BAC，
∴$\frac{S_{\triangle BFP}}{S_{\triangle BAC}}$ = ($\frac{x}{2}$)².
∵$S_{\triangle ABC}$ = 1，
∴$S_{\triangle BFP}$ = $\frac{x²}{4}$，同理$S_{\triangle PEC}$ = ($\frac{2 - x}{2}$)²，
∴y = 1 - $\frac{x²}{4}$ - $\frac{4 - 4x + x²}{4}$，
∴y = -$\frac{x²}{2}$ + x　
(2)上述函数有最大值，最大值为$\frac{1}{2}$；理由如下:
∵y = -$\frac{x²}{2}$ + x = -$\frac{1}{2}$(x - 1)² + $\frac{1}{2}$，-$\frac{1}{2}$＜0，
∴y有最大值，
∴当x = 1时，y有最大值，最大值为$\frac{1}{2}$