《2025年伴你学九年级数学下册苏科版》

2. 凸透镜成像的光路如图所示，AD//l//BC. 若物体到焦点F₁的水平距离HF₁与焦点F₁到凸透镜光心的距离F₁O的比为5∶4，则物体被缩小到原来的(　　　)
A. $\frac{4}{5}$ B. $\frac{2}{5}$ C. $\frac{4}{9}$ D. $\frac{5}{9}$
　　　

答案： A

3. 如图，小强和小华站在路灯下，小强的身高EF = 1.8 m，小华的身高MN = 1.5 m，他们的影子恰巧等于各自的身高，即BF = 1.8 m，CN = 1.5 m，且两人相距4.7 m. 求路灯AD的高度.
　　　　　　　

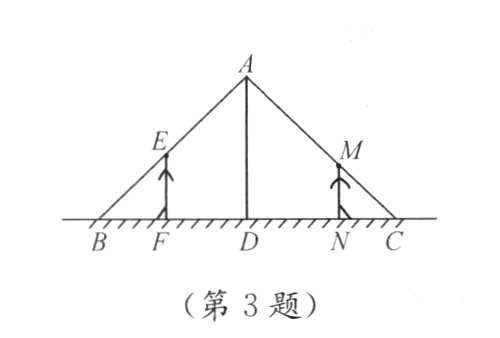
答案： 4m

1. 如图，两盏高度相同的路灯A、B底部之间的距离是30 m. 某天晚上，当小华走到距路灯B的底部5 m处时，发现自己的影子顶部正好接触路灯B的底部. 已知小华的身高为1.5 m，那么路灯B的高为________ m.
　　　　　　　

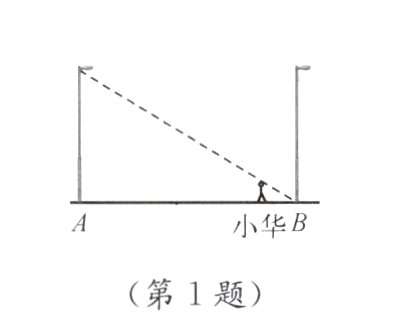
答案： 9

2. 如图，圆桌正上方的灯泡(可看作一个点)发出的光照射桌面后，在地面上形成圆形的影子. 已知桌面的直径为1.2 m，桌面距离地面1 m. 若灯泡距离地面3 m，则地面上圆形的影子的面积为(　　　)
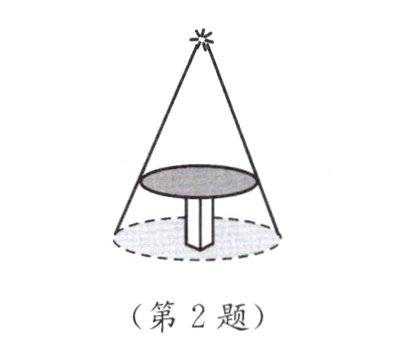
A. 0.36π m² B. 0.81π m² C. 2π m² D. 3.24π m²
　　　　　　　

答案： B

3. 学习了相似三角形的知识后，小明想利用路灯的光线测量一路灯的高度，并作出了示意图. 如图，路灯杆顶(点P)距地面若干米，身高为1.6 m的小明站在距路灯底部(点O)20 m的点A时，身影的长度AM为5 m.
(1) 请帮助小明求出路灯杆顶距地面的高度；
(2) 若身高为1.5 m的小龙站在直线OA上的点C时，测得他与小明的距离AC为7 m，求此时小龙影子的长度.
　　　　　　　　　　　　　　　　　　　　　　　　　　

答案：
(1) $\because AB\perp OM,PO\perp OM,\therefore \triangle MAB\sim\triangle MOP.\therefore \frac{AB}{OP}=\frac{AM}{OM}.$
$\therefore \frac{1.6}{OP}=\frac{5}{20 + 5}.\therefore OP = 8$，即路灯杆顶距地面的高度为8m
(2) $\because CD\perp OM,PO\perp OM,\therefore \triangle NCD\sim\triangle NOP.\therefore \frac{CD}{OP}=\frac{CN}{ON}.\because OC = OA - AC = 20 - 7 = 13,CD = 1.5,OP = 8,\therefore \frac{1.5}{8}=\frac{CN}{13 + CN}.\therefore CN = 3$，即小龙身影的长度为3m