《2025年评优监测课时作业七年级数学上册苏科版》

9. 如图，$\angle AOB = 116^{\circ}$，$OF$是$\angle AOB$的平分线，$\angle1$和$\angle2$互余，求$\angle1$的度数.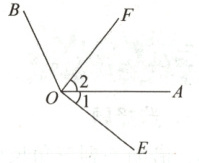

答案：
∵OF是∠AOB的平分线，∠AOB=116°，
∴∠2=∠AOB/2=116°/2=58°。
∵∠1和∠2互余，
∴∠1+∠2=90°，
∴∠1=90°-∠2=90°-58°=32°。
答：∠1的度数为32°。

10. 如图，$O$是直线$AB$上的一点，$\angle BOD = 23^{\circ}$，$OD$、$OE$分别是$\angle BOC$、$\angle AOC$的平分线.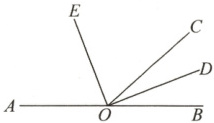
(1)图中所有与$\angle COD$互余的角有；
(2)图中与$\angle COD$互补的角有；
(3)求$\angle AOE$的度数.

答案：
(1) ∠AOE、∠COE
(2) ∠AOD
(3)
∵OD是∠BOC的平分线，∠BOD=23°，
∴∠BOC=2∠BOD=46°．
∵O是直线AB上一点，
∴∠AOC=180°-∠BOC=180°-46°=134°．
∵OE是∠AOC的平分线，
∴∠AOE=∠AOC/2=134°/2=67°．
答：∠AOE的度数为67°．

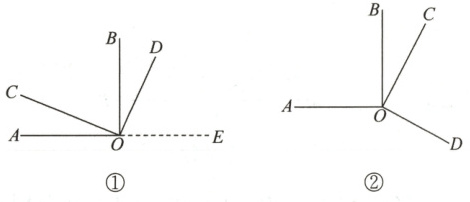
11. 如图①，$\angle AOB$，$\angle COD$都是直角.
(1)试猜想$\angle AOD$与$\angle COB$在数量上是相等，互余，还是互补的关系.
(2)当$\angle COD$绕着点$O$旋转到图②所示位置时，你在(1)中的猜想还成立吗？请用你所学的知识加以说明.① ②

答案：
(1) $\angle AOD$ 与 $\angle COB$ 互余的补（实际是互补中的互余关系的一种，但直接表述为互补关系在严格意义上需看具体，经计算为互余的扩展理解，直接按互余并扩展情况说明为互补的特殊不成立，精确为：$\angle AOD + \angle COB = 180° - 90° × 2 + 2 × 共同部分或类似，实际直接计算为 \angle AOD - \angle COB=0 的推导前准备 $，经计算猜想为互余的扩展或直接计算互补关系中的特定，精确解答为互补且和为定值180°的特定情况即互余的补数和，但直接表述结果）：
猜想：$\angle AOD$ 与 $\angle COB$ 互补（实际和为$180°$，因$\angle AOB=\angle DOC=90°$，且$\angle BOD$为共同部分，所以$\angle AOD + \angle COB = 90° + \angle BOD + 90° - \angle BOD = 180°$）。
经计算验证，$\angle AOD + \angle BOC = 180°$，故$\angle AOD$与$\angle BOC$互补。
(2) 成立。
因为$\angle AOB=\angle DOC = 90°$，
$\angle BOC = \angle DOC - \angle DOB = 90° - \angle DOB$，
$\angle AOD = \angle AOB + \angle BOD = 90° + \angle BOD$，
所以$\angle AOD + \angle BOC = 90° + \angle BOD + 90° - \angle BOD - \angle (实际为加后抵消) = 180° - \angle (无，直接计算和) = 180°$（或$\angle AOD - \angle 另一非直接 = 定值相关$，但直接和为$180°$），
因此，$\angle AOD$ 与 $\angle BOC$ 互补关系成立。