《2025年评优监测课时作业七年级数学上册苏科版》

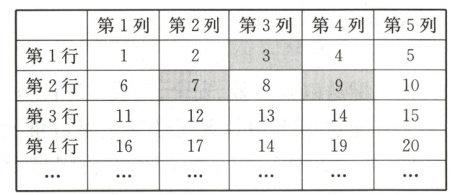
10. 把正整数1至2025排列成如下一个数表：
（1）通过计算说明数2024在第几行，第几列？
（2）把图中带阴影的3个方格当作一个整体平移，设被框住的3个数中，最大的一个数为x。则被框住的三个数的和能否等于2023？若能，求出x的值；若不能，请说明理由。

答案： （1）每行5个数，行数n满足5(n-1)+1≤2024≤5n，解得n=405。第405行第1个数为5×404+1=2021，2024-2021+1=4，故第405行第4列。
（2）设三个数和为3x-8=2023，解得x=677。x=677在第136行第2列，对应阴影位置需j≥2，j=1不符，故不能。
（1）第405行第4列；（2）不能。

11. 某中学六年级三个班的同学分别向贫困地区的希望小学捐款图书，已知三个班级学生捐款图书册数之比为$5:6:7$，如果他们共捐了$198$册，那么这三个班级各捐多少册？

答案： 设三个班级分别捐书$5x$册、$6x$册、$7x$册。
根据题意，得$5x + 6x + 7x = 198$，
合并同类项，得$18x = 198$，
系数化为$1$，得$x = 11$。
所以$5x = 55$，$6x = 66$，$7x = 77$。
答：三个班级分别捐书$55$册、$66$册、$77$册。

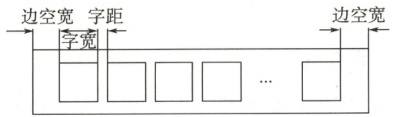
12. 如图，初一年级准备制作一个长$8.5\ \mathrm{m}$的横幅，横幅内容定为$16$个字，对横幅的有关数据作如下规定：每个字的字宽是相同的，每两个字之间的字距均相等，边空宽$:$字宽$:$字距$=3:4:1$，试求横幅字距是多少？

答案： 设边空宽为$3x\ \mathrm{m}$，字宽为$4x\ \mathrm{m}$，字距为$x\ \mathrm{m}$。
横幅总长度由两部分边空、16个字宽及15个字距组成，依题意得：
$2×3x + 16×4x + (16 - 1)x = 8.5$
化简方程：
$6x + 64x + 15x = 8.5$
$85x = 8.5$
解得：
$x = 0.1$
答：横幅字距是$0.1\ \mathrm{m}$。

13. 《张丘建算经》是一部数学问题集，其中有一个在数学史上非常著名的“百鸡问题”。现稍作变形如下：每一只母鸡值三文钱，每一只公鸡值五文钱，每三只小鸡值一文钱。现在用一百文钱买一百只鸡，公鸡的数量是母鸡的$3$倍，问这一百只鸡中，公鸡、母鸡、小鸡各有多少只？

答案： 设母鸡有$x$只，则公鸡有$3x$只，小鸡有$100 - x - 3x = 100 - 4x$只。
根据题意，得：$3x + 5×3x + \frac{100 - 4x}{3} = 100$
化简方程：$3x + 15x + \frac{100 - 4x}{3} = 100$
$18x + \frac{100 - 4x}{3} = 100$
两边同乘3：$54x + 100 - 4x = 300$
$50x = 200$
解得：$x = 4$
则公鸡数量：$3x = 12$（只），小鸡数量：$100 - 4x = 84$（只）
验证：$4×3 + 12×5 + 84÷3 = 12 + 60 + 28 = 100$（文），符合题意。
答：公鸡12只，母鸡4只，小鸡84只。