《2025年评优监测课时作业七年级数学上册苏科版》

8. 如图，正方形的边长为2，则图中阴影部分的面积之和等于.

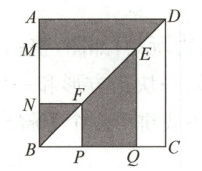
答案： 2

9. 用数学的眼光去观察问题，你会发现很多图形都能看成是动静结合，舒展自如的.下面所给的三排图形都存在着某种联系，用线将它们连起来.

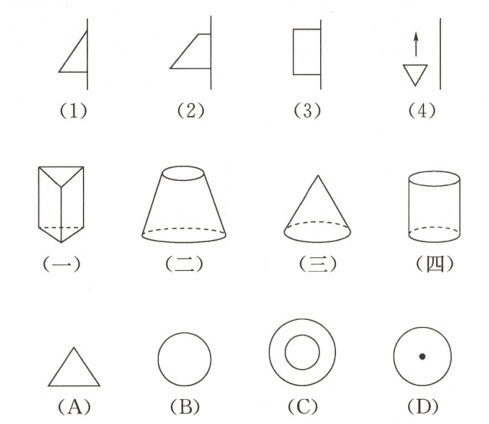
答案：
(1)-(一)-A
(2)-(二)-C
(3)-(四)-B
(4)-(三)-D

10. 按下列作图步骤，依次在图形B,C,D中涂上阴影：将图形A平移得到图形B;将图形B沿图中虚线翻折得到图形C;将图形C沿其右下方的顶点顺时针旋转$90°$得到图形D.

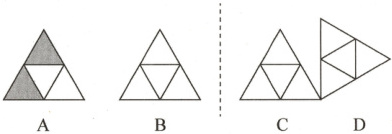
答案： A 图：正三角形内部由三条线段连接各边中点所形成的内部小三角形为阴影部分；
B 图：在 A 图的基础上保持不变，整个正三角形及内部图形位置不变，阴影部分位置也不变；
C 图：将 B 图沿图中虚线（垂直中线）翻折后，阴影部分位置对称到另一半对应的三角形内部；
D 图：将 C 图沿其右下方的顶点顺时针旋转$90°$，阴影部分移动到右上方三角形内对应的三角形中。
根据分析，在B图中，阴影部分和A图相同，不需要改变；
在C图中，阴影部分被垂直中线对称翻折，所以阴影部分移动到另一半对应的三角形中；
在D图中，阴影部分被顺时针旋转$90°$，所以阴影部分移动到右上方对应的三角形中。
选择D选项。

11. 已知长方形的长为8cm，宽为6cm，将其绕它的一边所在的直线旋转一周，得到一个立体图形.
(1) 得到几何图形的名称为，这个现象用数学知识解释为.
(2) 求此几何体的体积(结果保留π).

答案：
(1)
第一个空：圆柱
第二个空：面动成体
(2)
当绕长边旋转时，底面半径$r = 6cm$，高$h = 8cm$，根据圆柱体积公式$V=\pi r^{2}h$，可得$V_1=\pi×6^{2}×8 = 288\pi(cm^{3})$；
当绕短边旋转时，底面半径$R = 8cm$，高$H = 6cm$，根据圆柱体积公式$V=\pi R^{2}H$，可得$V_2=\pi×8^{2}×6 = 384\pi(cm^{3})$。
综上，此几何体体积为$288\pi cm^{3}$或$384\pi cm^{3}$。