《2025年评优监测课时作业七年级数学上册苏科版》

9. 甲、乙、丙、丁四位同学围成一圈依序循环报数.规定：① 甲、乙、丙、丁首次报出的数依次为 1,2,3,4，接着甲报 5，乙报 6⋯⋯每位同学报出的数比前一位同学报出的数大 1，按此规律，当报出的数是 50 时，报数结束；② 若报出的数是 3 的倍数，则报该数的同学需拍手一次.在此过程中，甲同学需拍几次手？

答案： 甲同学报数规律：首项为1，公差为4的等差数列，通项公式为$a_n = 4n - 3$（$n$为正整数）。
1. 确定甲报出的数：令$4n - 3 \leq 50$，解得$n \leq 13.25$，故$n = 1,2,·s,13$，甲报的数为：1,5,9,13,17,21,25,29,33,37,41,45,49。
2. 找出3的倍数：在上述数中，3的倍数为9,21,33,45，共4个。
结论：甲同学需拍手4次。
4

10. 如图是某商品包装盒上标签的部分内容，请你根据该内容确定这个商品包装盒的质量与体积.

答案： 答案略

11. 如图是某电器行的促销动传单.已知促销第一天美食牌微波炉卖出 10 台，且其销售额为 61 000 元.若活动期间此款微波炉总共卖出 50 台，则这些微波炉的总销售额为多少元？

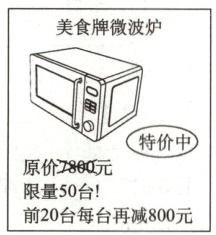
答案： 设特价为每台$x$元，前20台单价为$(x - 800)$元。
第一天卖出10台（属前20台），销售额61000元，可得：
$10(x - 800) = 61000$
解得$x - 800 = 6100$，$x = 6900$。
前20台单价：$6900 - 800 = 6100$元；
后$50 - 20 = 30$台单价：6900元。
总销售额：$20×6100 + 30×6900 = 122000 + 207000 = 329000$元。
答：这些微波炉的总销售额为329000元。