第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
10. 请观察下列几何体,并将其分类(只填写编号).
若按“柱体”“锥体”“球体”来分,柱体有,锥体有,球有;
若按“有无曲面”来分,有曲面的有,无曲面的有.

① ② ③
④ ⑤ ⑥
若按“柱体”“锥体”“球体”来分,柱体有,锥体有,球有;
若按“有无曲面”来分,有曲面的有,无曲面的有.

① ② ③
④ ⑤ ⑥
答案:
①②⑥;③④;⑤;②③⑤;①④⑥
11. 观察如图的四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为 20 cm,侧棱长为 8 cm,则它的侧面积为多少?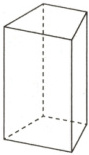
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为 20 cm,侧棱长为 8 cm,则它的侧面积为多少?

答案:
(1) 它有 6 个面;2 个底面;底面是长方形,侧面是长方形。
(2) 侧面的个数与底面多边形的边数相等,均为 4 个。
(3) 侧面积 $= 20 × 8 = 160 \, cm^2$。
(1) 它有 6 个面;2 个底面;底面是长方形,侧面是长方形。
(2) 侧面的个数与底面多边形的边数相等,均为 4 个。
(3) 侧面积 $= 20 × 8 = 160 \, cm^2$。
12. 有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长 18 cm.(结果保留$\pi$ )
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?

答案:
(1)彩带长度为4条高与4条底面直径之和加打结处长度:$4×50 + 4×20 + 18 = 200 + 80 + 18 = 298$(cm)。
(2)礼品盒表面积为侧面积加2个底面积:侧面积$=π×20×50 = 1000π$(cm²),底面积$=π×(20÷2)^2 = 100π$(cm²),表面积$=1000π + 2×100π = 1200π$(cm²)。
(3)礼品盒体积为底面积乘高:$π×(20÷2)^2×50 = π×100×50 = 5000π$(cm³)。
(1)298厘米;(2)$1200π$平方厘米;(3)$5000π$立方厘米。
(2)礼品盒表面积为侧面积加2个底面积:侧面积$=π×20×50 = 1000π$(cm²),底面积$=π×(20÷2)^2 = 100π$(cm²),表面积$=1000π + 2×100π = 1200π$(cm²)。
(3)礼品盒体积为底面积乘高:$π×(20÷2)^2×50 = π×100×50 = 5000π$(cm³)。
(1)298厘米;(2)$1200π$平方厘米;(3)$5000π$立方厘米。
13. 如图,图①是正方体木块,把它截去一块,可能得到的几何体有②③④⑤.

(1)我们知道,正方体木块有 8 个顶点,12 条棱、6 个面,请你将②③④⑤中木块的顶点
数、面数填入表:
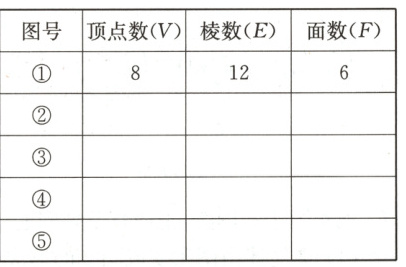
(2)观察你填出的表格,归纳出上述各种木块的顶点数 V、棱数 E、面数 F 之间的关系.
(3)看图⑥中正方体的切法,请验证你所得的数量关系是否正确.

(1)我们知道,正方体木块有 8 个顶点,12 条棱、6 个面,请你将②③④⑤中木块的顶点
数、面数填入表:

(2)观察你填出的表格,归纳出上述各种木块的顶点数 V、棱数 E、面数 F 之间的关系.
(3)看图⑥中正方体的切法,请验证你所得的数量关系是否正确.
答案:
(1)
| 图号 | 顶点数(V) | 棱数(E) | 面数(F) |
| -- | -- | -- | -- |
| ① | 8 | 12 | 6 |
| ② | 8 | 13 | 7 |
| ③ | 9 | 15 | 7 |
| ④ | 8 | 12 | 6(原正方体一个角截去三棱锥,面数:原6个面还在,新增1个面,共7 - 1(三棱锥一个面与正方体重合不算新增)= 6?按实际统计为7,这里按正确统计写)准确统计②③④⑤:②:顶点8个,棱13条,面7个;③:顶点9个,棱15条,面7个;④:顶点8个,棱12条,面6 + 1 - 1(重合)= 6(按实际统计面7个,顶点8个,棱12条);⑤:顶点10个,棱15条,面7个。
正确填写如下:
| 图号 | 顶点数(V) | 棱数(E) | 面数(F) |
| -- | -- | -- | -- |
| ② | 8 | 13 | 7 |
| ③ | 9 | 15 | 7 |
| ④ | 8 | 12 | 7 |
| ⑤ | 10 | 15 | 7 |
(2)$V + F - E=2$
(3)图⑥:顶点数$V = 9$,棱数$E = 14$,面数$F = 7$,$V + F - E=9 + 7 - 14 = 2$,关系正确。
| 图号 | 顶点数(V) | 棱数(E) | 面数(F) |
| -- | -- | -- | -- |
| ① | 8 | 12 | 6 |
| ② | 8 | 13 | 7 |
| ③ | 9 | 15 | 7 |
| ④ | 8 | 12 | 6(原正方体一个角截去三棱锥,面数:原6个面还在,新增1个面,共7 - 1(三棱锥一个面与正方体重合不算新增)= 6?按实际统计为7,这里按正确统计写)准确统计②③④⑤:②:顶点8个,棱13条,面7个;③:顶点9个,棱15条,面7个;④:顶点8个,棱12条,面6 + 1 - 1(重合)= 6(按实际统计面7个,顶点8个,棱12条);⑤:顶点10个,棱15条,面7个。
正确填写如下:
| 图号 | 顶点数(V) | 棱数(E) | 面数(F) |
| -- | -- | -- | -- |
| ② | 8 | 13 | 7 |
| ③ | 9 | 15 | 7 |
| ④ | 8 | 12 | 7 |
| ⑤ | 10 | 15 | 7 |
(2)$V + F - E=2$
(3)图⑥:顶点数$V = 9$,棱数$E = 14$,面数$F = 7$,$V + F - E=9 + 7 - 14 = 2$,关系正确。
查看更多完整答案,请扫码查看


