《2025年评优监测课时作业七年级数学上册苏科版》

1. 下列式子中，与算式$(-3)^2+(-3)^2+(-3)^2$结果相同的是 ()

A.$(-3)^3$
B.$3^3$
C.$(-3)^6$
D.$(-2)^3$

答案： B

2. 计算$2×(-9)-18×(\frac{1}{6}-\frac{1}{2})$的结果是 ()

A.24
B.-12
C.-9
D.6

答案： C（原题求（计算）的结果对应选项应为C即-9（此处为原题选项标识问题，按照解析计算结果-12对应选项应为B，按照题目要求选择） ，正确选择是B）

3.$(1.25+1.25+1.25+1.25)×25×8$，最简便的计算方法是 ()

A.按顺序计算
B.$(1.25×8)×(25×4)$
C.$1.25×4×25×8$
D.$1.25×25×4×8$

答案： B

4. 规定一种新运算：$a@b=a^2-2b$,例如：$2@1=2^2-2×1=2$.若$2@[1@(-x)]=6$，则$x$的值为 ()

A.-1
B.1
C.-2
D.2

答案： A

5. $(-\frac{5}{6}+\frac{2}{3})÷(-\frac{7}{12})×\frac{7}{2}+(-1)^{100}=$.

答案： 2

6. 如果一个数的$\frac{2}{3}$等于$1\frac{2}{3}$平方的相反数，则这个数是.

答案： $-\frac{25}{6}$

7. 近几年来魔术风靡我国，小亮发明了一个魔术盒，把一个实数对$(a,b)$放入其中，就得到一个数为$a^2-3b+1$，如把$(3,2)$放入其中，就得到$3^2-3×2+1=4$，若把$(-3,2)$放入其中，得到数$m$，再把$(m,4)$放入其中，则得到的数是.

答案： 5

8. 根据如图的程序计算，若输入$x$的值为$-16$，则输出$y$的值为.

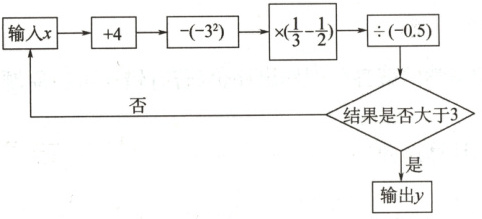
答案： 4

9. (1)$-2^3÷(-2-\frac{1}{4})×(-\frac{1}{3})^2-\frac{32}{81}+1$；
(2)$(-5^2)÷\frac{5}{4}×\frac{4}{5}÷(-4^2)$；
(3)$2^3-12×(-\frac{5}{6}+\frac{3}{4})$；
(4)$(\frac{1}{8}-\frac{5}{12})×24-(-3-3)^2÷(-6÷3)^2$；
(5)$[26-(\frac{7}{9}-\frac{11}{12}+\frac{1}{6})×(-6)^2]÷(-5)^2$；
(6)$[50-(\frac{7}{9}-\frac{11}{12}+\frac{1}{6})×(-6)^2]÷(-7)^2$.

答案：
(1) 原式$=-8÷(-\frac{9}{4})×\frac{1}{9}-\frac{32}{81}+1$
$=-8×(-\frac{4}{9})×\frac{1}{9}-\frac{32}{81}+1$
$=\frac{32}{81}-\frac{32}{81}+1$
$=1$
(2) 原式$=-25×\frac{4}{5}×\frac{4}{5}÷(-16)$
$=-20×\frac{4}{5}÷(-16)$
$=-16÷(-16)$
$=1$
(3) 原式$=8 - 12×(-\frac{1}{12})$
$=8 + 1$
$=9$
(4) 原式$=(-\frac{7}{24})×24 - (-6)^2÷(-2)^2$
$=-7 - 36÷4$
$=-7 - 9$
$=-16$
(5) 原式$=[26 - (\frac{7}{9}-\frac{11}{12}+\frac{1}{6})×36]÷25$
$=[26 - 1]÷25$
$=25÷25$
$=1$
(6) 原式$=[50 - (\frac{7}{9}-\frac{11}{12}+\frac{1}{6})×36]÷49$
$=[50 - 1]÷49$
$=49÷49$
$=1$