《2025年绩优课堂高效提升满分备考九年级数学全一册人教版》

9. (2024·石家庄一模)某学校射击队计划从甲、乙两名运动员中选取一名队员代表该校参加比赛,在选拔过程中,每名选手射击 10 次,根据甲、乙队员成绩绘制了如图 1,图 2 所示的统计图:
甲队员成绩条形统计图
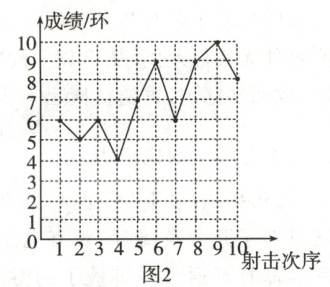
乙队员成绩折线统计图
并求得了乙队员 10 次射击成绩的平均数和方差:
$\overline{x}_{乙}=7$ 环,$s^{2}_{乙}=\frac{1}{10}[3×(6 - 7)^{2}+(5 - 7)^{2}+(4 - 7)^{2}+(7 - 7)^{2}+2×(9 - 7)^{2}+(10 - 7)^{2}+(8 - 7)^{2}]=3.4$.
(1)甲队员选拔赛成绩的众数是环,乙队员选拔赛成绩的中位数是环;7和86.5
(2)求甲队员 10 次射击成绩的平均数和方差,根据甲、乙两名队员的选拔赛成绩.你推荐谁代表学校参加比赛,并说明理由;
(3)为提升射击队技战术水平,学校决定除甲、乙外,再从射击队其他 5 名队员(三名男生,两名女生)中随机选出两名队员一同前往观看比赛,请你用画树状图或列表的方法求出恰好选出一名男生和一名女生的概率.

答案： 9.解：
(1)7和8,6.5；
$(2)x_{甲}=\frac{1}{10}(6 + 7×3 + 8×3 + 9 + 10×2)=8($环)，
$s_{甲}^2=\frac{1}{10}[(6 - 8)^2 + 3(7 - 8)^2 + 3(8 - 8)^2 + (9 - 8)^2 + 2(10 - 8)^2]=1.6；$
推荐甲参加比赛；
甲10次射击成绩的平均数高于乙，方差小于乙，所以甲的成绩更好更稳定.
$(3)\frac{3}{5}$

10. 某孵化场孵化出 1000 只小鸡,在 60 只上做记号,再放入鸡群中让其充分跑散,再任意抓出 50 只,其中做有记号的大约有(D)

A.40 只
B.25 只
C.15 只
D.3 只

答案： 10.D

11. 如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是(D)

A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{2}$
D.1

答案： 11.D

12. 【关注数学文化】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为 3:4,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.

答案： $12.\frac{24}{25}$