《2025年绩优课堂高效提升满分备考九年级数学全一册人教版》

10. 若$y = (m - 1)x^{m^{2} - 2}$是关于$x$的反比例函数关系式，则$m =$-1，此函数的解析式是y=-$\frac{2}{x}$。

答案： 10.-1 y=-$\frac{2}{x}$

11. 某地计划修建铁路$l$千米，铺轨天数为$t$(天)，每日铺轨量为$s$(千米/天)，则在下列三个结论中，正确的是(A)
①当$l$一定时，$t$是$s$的反比例函数；
②当$t$一定时，$l$是$s$的反比例函数；
③当$s$一定时，$l$是$t$的反比例函数。

A.仅①
B.仅②
C.仅③
D.①②③

答案： 11.A

12. 已知$y = - \frac{k - 1}{x}$是关于$x$的反比例函数，则$k$的取值范围是k≠1；当$x = - 3$时，$y$的值为$5$，则$k =$16。

答案： 12.$k\neq1$ 16

13. 用电器的电流$I$、电阻$R$、电功率$P$之间满足关系式$P = I^{2}R$。已知$P = 5\ W$，填写下表并回答问题。

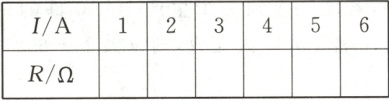
(1)变量$R$是变量$I$的函数吗？
(2)变量$R$是变量$I$的反比例函数吗？

答案： 13.解：填表略.
(1)因为P=$I^{2}$R,P=5,所以R=$\frac{5}{I^{2}}$.所以R是I
的函数.
(2)因为R=$\frac{5}{I^{2}}$不满足y=$\frac{k}{x}$(k为常数，且k≠0)的形式,所
以R不是I的反比例函数.

14. 已知$y = (m^{2} + 2m)x^{m^{2} + m - 1}$。
(1)当$m$为何值时，$y$是$x$的正比例函数？
(2)当$m$为何值时，$y$是$x$的二次函数？
(3)当$m$为何值时，$y$是$x$的反比例函数？

答案： 14.
(1)m=1
(2)m=$\frac{-1+\sqrt{13}}{2}$或$\frac{-1-\sqrt{13}}{2}$
(3)m=-1

15. 已知$y = y_{1} - y_{2}$，其中$y_{1}$是$x$的反比例函数，$y_{2}$是$x$的正比例函数，且当$x = 1$时，$y = 3$；当$x = - 2$时，$y = - 15$。
(1)求$y$与$x$之间的函数解析式；
(2)当$x = 2$时，$y$的值是多少？

答案： 15.解：
(1)设$y_{1}=\frac{k_{1}}{x}$,$y_{2}=k_{2}x(k_{1},k_{2}$均不为0),所以y=$y_{1}-y_{2}=\frac{k_{1}}{x}-k_{2}x$.
因为当x=1时,y=3;当x=-2时,y=-15,所以
$\begin{cases}k_{1}-k_{2}=3\frac{k_{1}}{-2}+2k_{2}=-15\end{cases}$ 解得$\begin{cases}k_{1}=-6\\k_{2}=-9\end{cases}$
所以y=$-\frac{6}{x}+9x$.
(2)当x=2时,y=$-\frac{6}{2}+9×2=15$.

16. 调查显示，某商场一款运动鞋的售价是销售量的反比例函数(调查获得的部分数据如下表)。

已知该运动鞋的进价为$180$元/双，要使该款运动鞋每天的销售利润达到$2400$元，则其售价应定为300元/双。

答案： 16.300