《2025年绩优课堂高效提升满分备考九年级数学全一册人教版》

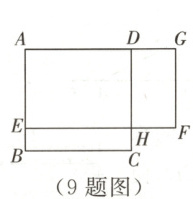
9. 某小区拆除自建房改建绿地。如图，自建房占地是边长为$20m$的正方形$ABCD$，改建的绿地是矩形$AEFG$，其中点$E$在$AB$上，点$G$在$AD$的延长线上，且$DG = 2BE$。如果设$BE$的长为$x$(单位：$m$)，绿地$AEFG$的面积为$y$(单位：$m^2$)，那么$y$与$x$的函数解析式为____，绿地$AEFG$的最大面积为____$m^2$。

答案： 9.y=-2x²+20x+400(0＜x＜20) 450

10. 如图，在边长为$6cm$的正方形$ABCD$中，点$E$，$F$，$G$，$H$分别从点$A$，$B$，$C$，$D$同时出发，均以$1cm/s$的速度向点$B$，$C$，$D$，$A$匀速运动。当点$E$到达点$B$时，四个点同时停止运动，在运动过程中，当运动时间为3$s$时，四边形$EFGH$的面积最小，其最小值是18$cm^2$。

答案： 10.3 18

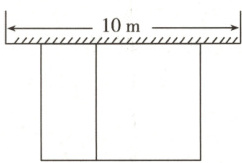
11. (2024·无锡)某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙(墙的长度为$10m$)，另外三面用栅栏围成，中间再用栅栏把它分成两个面积为$1:2$的矩形，已知栅栏的总长度为$24m$，设较小矩形的宽为$x m$(如图)。
(1)若矩形养殖场的总面积为$36m^2$，求此时$x$的值；
(2)当$x$为多少时，矩形养殖场的总面积最大？最大值为多少？

答案： 11.解：
(1)根据题意可得：$3x·\frac{24-3x}{3}=36，$
化简得：x²-8x+12=0，
解得x₁=2，x₂=6(不合题意，舍去).
答：若矩形养殖场的总面积为36m²，此时x的值为2.
(2)设矩形养殖场的总面积为S m².
根据题意可得：
S=-3x²+24x=-3(x-4)²+48.
由二次函数图象性质可知，当x＜4时，S随着x的增大而增大，
∵3x≤10，即$x≤\frac{10}{3}，$
∴当$x=\frac{10}{3}$时，S的最大值为$\frac{140}{3}.$
答：当x为$\frac{10}{3}$时，矩形养殖场的总面积最大为$\frac{140}{3}m².$

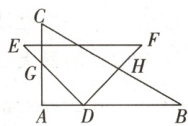
12. 一副三角板($\triangle ABC$与$\triangle DEF$)如图放置，点$D$在$AB$边上滑动，$DE$交$AC$于点$G$，$DF$交$BC$于点$H$，且在滑动过程中始终保持$DG = DH$。若$AC = 2$，则$\triangle BDH$面积的最大值是(C)

A.$3$
B.$3\sqrt{3}$
C.$\frac{3}{2}$
D.$\frac{3\sqrt{3}}{2}$

答案： 12.C