第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
1. 绿苑小区在做规划设计时,准备在两幢楼房之间设置一块面积为 $ 900 \, m^2 $ 的矩形绿地,并且长比宽多 $ 10 \, m $。设绿地的宽为 $ x \, m $,则长为
(x+10)
m。根据题意,可列方程为x(x+10)=900
。
答案:
1.(x+10) x(x+10)=900
2. (2024·青海)如图,小明同学用一张长 $ 11 \, cm $,宽 $ 7 \, cm $ 的矩形纸板制作一个底面积为 $ 21 \, cm^2 $ 的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计)。设剪去的正方形边长为 $ x \, cm $,则可列出关于 $ x $ 的方程为

(11-2x)(7-2x)=21
。
答案:
2.(11-2x)(7-2x)=21
3. (2023·衡阳)如图,学校课外生物小组的试验园地的形状是长 $ 35 \, m $、宽 $ 20 \, m $ 的矩形。为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为 $ 600 \, m^2 $,则小道的宽为多少米?若设小道的宽为 $ x \, m $,则根据题意,列方程为(
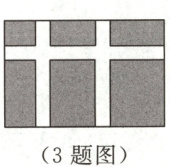
A.$ 35 × 20 - 35x - 20x + 2x^2 = 600 $
B.$ 35 × 20 - 35x - 2 × 20x = 600 $
C.$ (35 - 2x)(20 - x) = 600 $
D.$ (35 - x)(20 - 2x) = 600 $
C
)
A.$ 35 × 20 - 35x - 20x + 2x^2 = 600 $
B.$ 35 × 20 - 35x - 2 × 20x = 600 $
C.$ (35 - 2x)(20 - x) = 600 $
D.$ (35 - x)(20 - 2x) = 600 $
答案:
3.C
【变式】如图,某单位准备在院内一块长 $ 30 \, m $、宽 $ 20 \, m $ 的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的部分种植花草。要使种植花草的面积为 $ 532 \, m^2 $,则小道进出口的宽度为
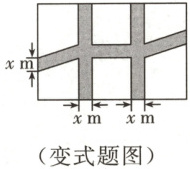
1
m。
答案:
【变式】1
4. (2023·郑州中原)如图,要利用一面墙(墙长为 $ 55 \, m $),用 $ 100 \, m $ 的围栏建羊圈,基本结构为三个大小相同的矩形。
(1)如果围成的总面积为 $ 400 \, m^2 $,求羊圈的边 $ AB $,$ BC $ 长各为多少;
(2)保持羊圈的基本结构,羊圈总面积是否可以达到 $ 800 \, m^2 $?请说明理由。

(1)如果围成的总面积为 $ 400 \, m^2 $,求羊圈的边 $ AB $,$ BC $ 长各为多少;
(2)保持羊圈的基本结构,羊圈总面积是否可以达到 $ 800 \, m^2 $?请说明理由。

答案:
4.解:
(1)设AB=x m,则BC=(100-4x)m,
∵100-4x≤55,
∴x≥11.25.
由题意知,x(100-4x)=400,即$x^{2}-25x+100=0,$
解得$x_{1}=20,x_{2}=5($舍),
∴AB=20m,BC=100-4×20=20(m).
答:羊圈的边AB长为20m,BC长为20m.
(2)不能.
理由:设AB=y m时,羊圈总面积可以达到$800m^{2},$
由题意,得y(100-4y)=800,
即$y^{2}-25y+200=0,$
∵a=1,b=-25,c=200,
∴$b^{2}-4ac=(-25)^{2}-4×1×200=-175<0,$
∴方程无实数根,
∴羊圈总面积不可能达到$800m^{2}.$
(1)设AB=x m,则BC=(100-4x)m,
∵100-4x≤55,
∴x≥11.25.
由题意知,x(100-4x)=400,即$x^{2}-25x+100=0,$
解得$x_{1}=20,x_{2}=5($舍),
∴AB=20m,BC=100-4×20=20(m).
答:羊圈的边AB长为20m,BC长为20m.
(2)不能.
理由:设AB=y m时,羊圈总面积可以达到$800m^{2},$
由题意,得y(100-4y)=800,
即$y^{2}-25y+200=0,$
∵a=1,b=-25,c=200,
∴$b^{2}-4ac=(-25)^{2}-4×1×200=-175<0,$
∴方程无实数根,
∴羊圈总面积不可能达到$800m^{2}.$
查看更多完整答案,请扫码查看


