第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
10. (2024·衡阳)如图,用一个半径为6cm的定滑轮拉动重物上升,滑轮旋转了120°,假设绳索粗细不计,且与滑轮之间没有滑动,则重物上升了

$4\pi$
cm。(结果保留π)
答案:
$10.4\pi$
11. (2023·青海)如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是(
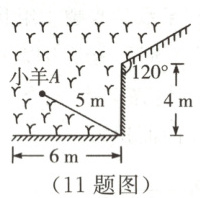
A.$\frac{17}{12}\pi$m²
B.$\frac{77}{12}\pi$m²
C.$\frac{25}{4}\pi$m²
D.$\frac{17}{6}\pi$m²
B
)
A.$\frac{17}{12}\pi$m²
B.$\frac{77}{12}\pi$m²
C.$\frac{25}{4}\pi$m²
D.$\frac{17}{6}\pi$m²
答案:
11.B
$12. $如图,点$A,$$B,$$C$都在方格纸的格点上,$△ABC$绕点$A$顺时针方向旋转$90°$后得到$△AB'C',$则点$B$运动的路径$\overset{\frown}{BB'}$的长为

$\frac{5\pi}{2}$
。 
答案:
$12.\frac{5\pi}{2}$
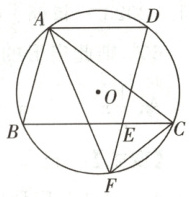
13. 如图,△ABC内接于⊙O,AD//BC交⊙O于点D,DF//AB交BC于点E,交⊙O于点F,连接AF,CF。
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求$\overset{\frown}{AC}$的长(结果保留π)。
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求$\overset{\frown}{AC}$的长(结果保留π)。

答案:
13.
(1) 证明:
∵ AD // BC,DF // AB,
∴ 四边形 ABED 是平行四边形,
∴ ∠B = ∠D.
又 ∠AFC = ∠B, ∠ACF = ∠D,
∴ ∠AFC = ∠ACF,
∴ AC = AF.
(2)解:连接 AO,CO, 由
(1)得 ∠AFC = ∠ACF,
又
∵$ ∠CAF = 30°, ∠AFC = \frac{180° - 30°}{2} = 75°,$
∴ ∠AOC = 2∠AFC = 150°.
∴ AC的长$ = \frac{150 × \pi × 3}{180} = \frac{5\pi}{2}$
(1) 证明:
∵ AD // BC,DF // AB,
∴ 四边形 ABED 是平行四边形,
∴ ∠B = ∠D.
又 ∠AFC = ∠B, ∠ACF = ∠D,
∴ ∠AFC = ∠ACF,
∴ AC = AF.
(2)解:连接 AO,CO, 由
(1)得 ∠AFC = ∠ACF,
又
∵$ ∠CAF = 30°, ∠AFC = \frac{180° - 30°}{2} = 75°,$
∴ ∠AOC = 2∠AFC = 150°.
∴ AC的长$ = \frac{150 × \pi × 3}{180} = \frac{5\pi}{2}$
14. (2023·淄博)如图,放置在直线l上的扇形OAB由图①滚动(无滑动)到图②,再由图②滚动到图③。若半径OA=2,∠AOB=45°,则点O所经过的最短路径的长是(
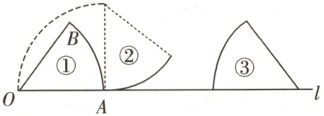
A.$2\pi + 2$
B.$3\pi$
C.$\frac{5\pi}{2}$
D.$\frac{5\pi}{2} + 2$
C
)
A.$2\pi + 2$
B.$3\pi$
C.$\frac{5\pi}{2}$
D.$\frac{5\pi}{2} + 2$
答案:
14.C
查看更多完整答案,请扫码查看


