第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
8.(2023·唐山玉田县期中)扬帆中学有一块长$30\ m$,宽$20\ m$的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度。设花带的宽度为$x\ m$,则可列方程为 (
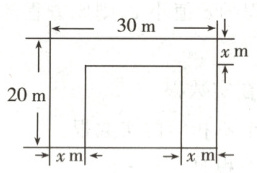
A.$(30 - x)(20 - x) = \frac{3}{4} × 20 × 30$
B.$(30 - 2x)(20 - x) = \frac{1}{4} × 20 × 30$
C.$30x + 2 × 20x = \frac{1}{4} × 20 × 30$
D.$(30 - 2x)(20 - x) = \frac{3}{4} × 20 × 30$
D
)
A.$(30 - x)(20 - x) = \frac{3}{4} × 20 × 30$
B.$(30 - 2x)(20 - x) = \frac{1}{4} × 20 × 30$
C.$30x + 2 × 20x = \frac{1}{4} × 20 × 30$
D.$(30 - 2x)(20 - x) = \frac{3}{4} × 20 × 30$
答案:
8.D
9.(2023·石家庄)现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,我市某快递公司,今年八月份与十月份完成投递的快递总件数分别为$10$万件和$12.1$万件。现假定该公司每月投递的快递总件数的增长率相同。
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递$0.6$万件,那么该公司现有的$21$名快递投递业务员能否完成今年十一月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递$0.6$万件,那么该公司现有的$21$名快递投递业务员能否完成今年十一月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
答案:
9.
(1)该快递公司投递总件数的月平均增长率为$10\%$。
(2)至少要增加$2$名业务员。
(1)该快递公司投递总件数的月平均增长率为$10\%$。
(2)至少要增加$2$名业务员。
$10.【$问题提出$】$在抗击新冠肺炎的斗争中,某中学响应政府$“$停课不停学$”$的号召,进行线上学习,九年级一班的全体同学在自主完成学习任务的同时,全班每两个同学都通过一次视频电话,彼此关怀,互相勉励,共同提高。若每两名同学之间仅通过一次视频电话,如何求全班$56$名同学共通过多少次电话呢$?$
$【$模型构建$】$用点$M_{1},M_{2},M_{3},·s,M_{56}$分别表示第$1,2,3,·s,56$名同学,把该班级人数$n$与视频通话次数$S$之间的关系用如下图所示的模型表示:
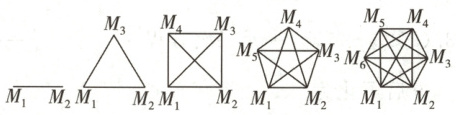
$【$问题解决$】$
$(1)$上图第五个图中$S$的值为
$(2)$通过探索发现,通话次数$S$与该班级人数$n$之间的关系式为
$(3)$若该班全体女生相互之间共通话$253$次,求该班有多少名女生。
$(4)$若该班数学兴趣小组的同学们,每两位同学之间互发一条微信问候,小明统计全组共发送微信$182$条,则该班数学兴趣小组的人数是
$【$模型构建$】$用点$M_{1},M_{2},M_{3},·s,M_{56}$分别表示第$1,2,3,·s,56$名同学,把该班级人数$n$与视频通话次数$S$之间的关系用如下图所示的模型表示:

$【$问题解决$】$
$(1)$上图第五个图中$S$的值为
$15$
; $(2)$通过探索发现,通话次数$S$与该班级人数$n$之间的关系式为
$S=\frac{n(n - 1)}{2}$
,则当$n = 56$时,对应的$S =$ $1540$
; $(3)$若该班全体女生相互之间共通话$253$次,求该班有多少名女生。
$(4)$若该班数学兴趣小组的同学们,每两位同学之间互发一条微信问候,小明统计全组共发送微信$182$条,则该班数学兴趣小组的人数是
$14$
。
答案:
10.解:
(1)15
(2)$S=\frac{n(n - 1)}{2}1540$
(3)设该班有$x$名女生,依题意,得$\frac{x(x - 1)}{2}=253$。
解得$x_1 = 23,x_2 = - 22$(舍去)。
答:该班有$23$名女生。
(4)14
(1)15
(2)$S=\frac{n(n - 1)}{2}1540$
(3)设该班有$x$名女生,依题意,得$\frac{x(x - 1)}{2}=253$。
解得$x_1 = 23,x_2 = - 22$(舍去)。
答:该班有$23$名女生。
(4)14
查看更多完整答案,请扫码查看


