《2025年绩优课堂高效提升满分备考九年级数学全一册人教版》

6. (2023·本溪)某网店销售一款市场上畅销的蒸蛋糕，进价为每个 40 元，在销售过程中发现，当这款蒸蛋器的销售单价为 60 元时，每星期卖出 100 个. 如果调整销售单价，每涨价 1 元，每星期就少卖出 2 个，现网店决定提价销售，设销售单价为 $ x $（元），每星期的销售量为 $ y $（个）.
(1) 请直接写出 $ y $（个）与 $ x $（元）之间的函数关系式；
(2) 当销售单价是多少元时，该网店每星期的销售利润是 2400 元？
(3) 当销售单价是多少元时，该网店每星期的销售利润最大？最大利润是多少元？

答案： 6.解：
(1)由题意，得$y = 100 - 2(x - 60) = - 2x + 220$.$\therefore y($个$)$与$x($元$)$之间的函数关系式是$y = - 2x + 220$.
(2)设利润为$W$，则$W = (x - 40)y = (x - 40)( - 2x + 220) =$
$- 2x^{2} + 300x - 8800$.
令$W = 2400$，则$- 2x^{2} + 300x - 8800 = 2400$，解得$x = 70$或
$x = 80$.
答：当销售单价为$70$元或$80$元时，该网店每星期的销售利润
是$2400$元.
(3)$W = - 2x^{2} + 300x - 8800 = - 2(x - 75)^{2} + 2450$.
$\because - 2 ＜ 0$，$\therefore$当$x = 75$时，$W$取最大值，最大值为$2450$.
答：当销售单价是$75$元时，该网店每星期的销售利润最大，最
大利润是$2450$元.

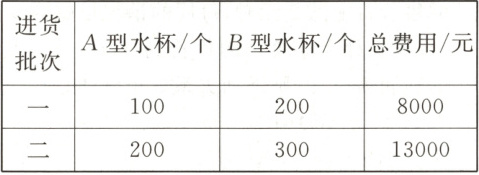
7. (2023·怀化)某超市从厂家购进 $ A $，$ B $ 两种型号的水杯，两次购进水杯的情况如表：
(1) $ A $，$ B $ 两种型号的水杯的进价分别为多少元？
(2) 在销售过程中，$ A $ 型水杯因为物美价廉而更受消费者喜欢. 为了增大 $ B $ 型水杯的销售量，超市决定对 $ B $ 型水杯进行降价销售，当销售价为 44 元时，每天可以售出 20 个，每降价 1 元，每天将多售出 5 个. 请问超市将 $ B $ 型水杯降价多少元时，每天售出 $ B $ 型水杯的利润达到最大？最大利润是多少？
(3) 该超市第三次进货时用 10000 元钱购进这两种水杯，如果每售出一个 $ A $ 型水杯可获利 10 元，每售出一个 $ B $ 型水杯可获利 9 元，超市决定每售出一个 $ A $ 型水杯，就为当地新冠疫情防控捐出 $ b $ 元用于购买防控物资. 若 $ A $，$ B $ 两种型号的水杯在全部售出的情况下，捐款后所得的利润始终不变，则此时 $ b $ 为多少？利润为多少？

答案： 7.解：
(1)设A型水杯的进价为$x$元，B型水杯的进价为$y$元，根
据题意，
得$\begin{cases}100x + 200y = 8000, \\200x + 300y = 13000,\end{cases}$解得$\begin{cases}x = 20, \\y = 30.\end{cases}$
答：A型水杯的进价为$20$元，B型水杯的进价为$30$元.
(2)设超市将B型水杯降价$m$元时，每天售出B型水杯的利润
为$W$元，根据题意，
得$W = (44 - m - 30)(20 + 5m) = - 5(m - 5)^{2} + 405$.
$\therefore$当$m = 5$时，$W$取最大值，最大值为$405$.
答：超市将B型水杯降价$5$元时，每天售出B型水杯的利润达
到最大，最大利润是$405$元.
(3)设总利润为$w$元，购进A型水杯$a$个，依题意，得$w =$
$(10 - b)a + 9 × \frac{10000 - 20a}{30} = (4 - b)a + 3000$.
$\because$捐款后所得的利润始终不变，$\therefore w$的值与$a$的值无关.
$\therefore 4 - b = 0$，解得$b = 4$.
$\therefore w = (4 - 4)a + 3000 = 3000$.
答：此时$b = 4$，利润为$3000$元.