第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
10. (2024·临沂)杠杆原理在生活中被广泛应用 (杠杆原理:阻力 $ × $ 阻力臂 $ = $ 动力 $ × $ 动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图 1). 制作方法如下:
第一步:在一根匀质细木杆上标上均匀的刻度 (单位长度 $ 1 cm $),确定支点 $ O $,并用细麻绳固定,在支点 $ O $ 左侧 $ 2 cm $ 的 $ A $ 处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为 $ 0.5 kg $ 的金属物体作为秤砣.
(1) 图 1 中,把重物挂在秤钩上,秤砣挂在支点 $ O $ 右侧的 $ B $ 处,秤杆平衡,就能称得重物的质量. 当重物的质量变化时,$ OB $ 的长度随之变化. 设重物的质量为 $ x kg $,$ OB $ 的长为 $ y cm $. 写出 $ y $ 关于 $ x $ 的函数解析式;若 $ 0 < y < 48 $,求 $ x $ 的取值范围;
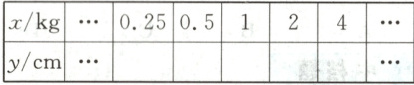
(2) 调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点 $ O $ 右侧的 $ B $ 处,使秤杆平衡,如图 2. 设重物的质量为 $ x kg $,$ OB $ 的长为 $ y cm $. 写出 $ y $ 关于 $ x $ 的函数解析式,完成下表,画出该函数的图象.


第一步:在一根匀质细木杆上标上均匀的刻度 (单位长度 $ 1 cm $),确定支点 $ O $,并用细麻绳固定,在支点 $ O $ 左侧 $ 2 cm $ 的 $ A $ 处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为 $ 0.5 kg $ 的金属物体作为秤砣.
(1) 图 1 中,把重物挂在秤钩上,秤砣挂在支点 $ O $ 右侧的 $ B $ 处,秤杆平衡,就能称得重物的质量. 当重物的质量变化时,$ OB $ 的长度随之变化. 设重物的质量为 $ x kg $,$ OB $ 的长为 $ y cm $. 写出 $ y $ 关于 $ x $ 的函数解析式;若 $ 0 < y < 48 $,求 $ x $ 的取值范围;
(2) 调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点 $ O $ 右侧的 $ B $ 处,使秤杆平衡,如图 2. 设重物的质量为 $ x kg $,$ OB $ 的长为 $ y cm $. 写出 $ y $ 关于 $ x $ 的函数解析式,完成下表,画出该函数的图象.



答案:
10.解:
(1)因为OA = 2cm,重物的质量为xkg,OB的长为ycm,秤砣的质量为0.5kg,所以2x = 0.5y,所以y = 4x。
因为4>0,所以y随x的增大而增大。
因为当y = 0时,x = 0;当y = 48时,x = 12,所以0<x<12。
(2)由题意得2×0.5 = xy,所以y = $\frac{1}{x}$。
当x = 0.25时,y = $\frac{1}{0.25}$ = 4;
当x = 0.5时,y = $\frac{1}{0.5}$ = 2;
当x = 1时,y = 1;当x = 2时,y = 0.5;当x = 4时,y = 0.25。完成表格:
x/kg … 0.25 0.5 1 2 4 …
y/cm … 4 2 1 0.5 0.25 …
作函数图象如图所示,

10.解:
(1)因为OA = 2cm,重物的质量为xkg,OB的长为ycm,秤砣的质量为0.5kg,所以2x = 0.5y,所以y = 4x。
因为4>0,所以y随x的增大而增大。
因为当y = 0时,x = 0;当y = 48时,x = 12,所以0<x<12。
(2)由题意得2×0.5 = xy,所以y = $\frac{1}{x}$。
当x = 0.25时,y = $\frac{1}{0.25}$ = 4;
当x = 0.5时,y = $\frac{1}{0.5}$ = 2;
当x = 1时,y = 1;当x = 2时,y = 0.5;当x = 4时,y = 0.25。完成表格:
x/kg … 0.25 0.5 1 2 4 …
y/cm … 4 2 1 0.5 0.25 …
作函数图象如图所示,

11. 方方驾驶小汽车从 $ A $ 地匀速行驶到 $ B $ 地,行驶里程为 $ 480 $ 千米. 设小汽车行驶时间为 $ t $ (时),行驶速度为 $ v $ (千米/时),且全程限定速度不超过 $ 120 $ 千米/时.
(1) $ v $ 关于 $ t $ 的函数解析式为 ,自变量的取值范围为.
(2) 已知方方上午 $ 8 $ 点驾驶小汽车从 $ A $ 地出发.
① 方方需在当天 $ 12 $ 点 $ 48 $ 分至 $ 14 $ 点(含 $ 12 $ 点 $ 48 $ 分和 $ 14 $ 点)间到达 $ B $ 地,求小汽车行驶速度 $ v $ 的取值范围;
② 方方能否在当天 $ 11 $ 点 $ 30 $ 分前到达 $ B $ 地?说明理由.
(1) $ v $ 关于 $ t $ 的函数解析式为 ,自变量的取值范围为.
v = $\frac{480}{t}$,t ≥ 4
(2) 已知方方上午 $ 8 $ 点驾驶小汽车从 $ A $ 地出发.
① 方方需在当天 $ 12 $ 点 $ 48 $ 分至 $ 14 $ 点(含 $ 12 $ 点 $ 48 $ 分和 $ 14 $ 点)间到达 $ B $ 地,求小汽车行驶速度 $ v $ 的取值范围;
② 方方能否在当天 $ 11 $ 点 $ 30 $ 分前到达 $ B $ 地?说明理由.
①根据题意,得4.8 ≤ t ≤ 6。因为480>0,所以$\frac{480}{6}$ ≤ v ≤ $\frac{480}{4.8}$,所以80 ≤ v ≤ 100。②方方不能在当天11点30分前到达B地。理由如下:若方方要在当天11点30分前到达B地,则t<3.5,所以v>$\frac{480}{3.5}$>120。所以方方不能在当天11点30分前到达B地。
答案:
11.解:
(1)v = $\frac{480}{t}$,t ≥ 4
(2)①根据题意,得4.8 ≤ t ≤ 6。因为480>0,所以$\frac{480}{6}$ ≤ v ≤ $\frac{480}{4.8}$,所以80 ≤ v ≤ 100。
②方方不能在当天11点30分前到达B地。
理由如下:若方方要在当天11点30分前到达B地,则t<3.5,所以v>$\frac{480}{3.5}$>120。所以方方不能在当天11点30分前到达B地。
(1)v = $\frac{480}{t}$,t ≥ 4
(2)①根据题意,得4.8 ≤ t ≤ 6。因为480>0,所以$\frac{480}{6}$ ≤ v ≤ $\frac{480}{4.8}$,所以80 ≤ v ≤ 100。
②方方不能在当天11点30分前到达B地。
理由如下:若方方要在当天11点30分前到达B地,则t<3.5,所以v>$\frac{480}{3.5}$>120。所以方方不能在当天11点30分前到达B地。
查看更多完整答案,请扫码查看


