第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
6 [2025 南阳宛城区模拟]如图,在 $7 × 7$ 的正方形网格中,每个小正方形的边长都为 1,点 $A,B,C,D,E,F$ 均在格点上,则到线段 $AB$ 的两个端点距离相等的点所在的直线是 ( )
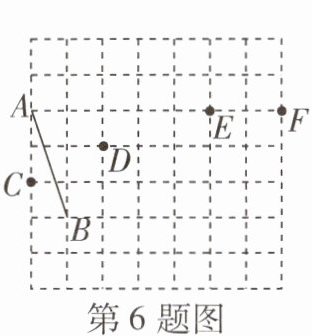
A.直线 $CD$
B.直线 $CE$
C.直线 $DE$
D.直线 $DF$

A.直线 $CD$
B.直线 $CE$
C.直线 $DE$
D.直线 $DF$
答案:
C 如图,连接BC,AD,BD,BE,BF。根据勾股定理,得BC=√(1²+1²)=√2,AD=BD=√(2²+1²)=√5,BE=√(3²+4²)=5,
∴AE=BE=5,
∴点D和点E在线段AB的垂直平分线上,
∴到线段AB的两个端点距离相等的点所在的直线是直线DE。
C 如图,连接BC,AD,BD,BE,BF。根据勾股定理,得BC=√(1²+1²)=√2,AD=BD=√(2²+1²)=√5,BE=√(3²+4²)=5,
∴AE=BE=5,
∴点D和点E在线段AB的垂直平分线上,
∴到线段AB的两个端点距离相等的点所在的直线是直线DE。

7 [2025 西安新城区爱知中学开学考试]在如图所示的网格中,小正方形的边长均为 1,$\triangle ABC$ 的顶点 $A,B,C$ 均在正方形格点上,则下列结论错误的是 ( )
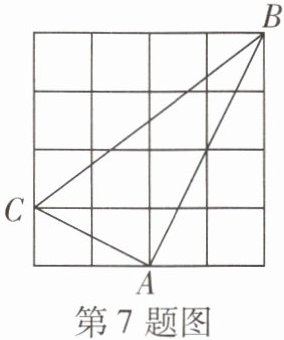
A.$AB^2 = 20$
B.$\angle BAC = 90^{\circ}$
C.$AC = \frac{5}{2}$
D.点 $A$ 到直线 $BC$ 的距离是 2

A.$AB^2 = 20$
B.$\angle BAC = 90^{\circ}$
C.$AC = \frac{5}{2}$
D.点 $A$ 到直线 $BC$ 的距离是 2
答案:
C 由题意得,AB²=2²+4²=20,AC=√(2²+1²)=√5,BC=√(3²+4²)=5,
∴AB²+AC²=BC²,
∴△ABC是直角三角形,且∠BAC=90°,故选项A,B正确,选项C错误;如图,过点A作AD⊥BC于点D,则(1/2)BC·AD=(1/2)AC·AB,即5AD=√20·√5=10,解得AD=2,
∴点A到直线BC的距离是2,故选项D正确。
C 由题意得,AB²=2²+4²=20,AC=√(2²+1²)=√5,BC=√(3²+4²)=5,
∴AB²+AC²=BC²,
∴△ABC是直角三角形,且∠BAC=90°,故选项A,B正确,选项C错误;如图,过点A作AD⊥BC于点D,则(1/2)BC·AD=(1/2)AC·AB,即5AD=√20·√5=10,解得AD=2,
∴点A到直线BC的距离是2,故选项D正确。

8 [2025 枣庄峄城区期中]平面内将长度为 8,5,6 的三根木棒按如图所示的方式连接成折线 $A \to B \to C \to D$,其中 $AB$ 可以绕点 $B$ 任意旋转,$\angle C = 90^{\circ}$,将点 $A,D$ 用绷直的皮筋连接. 设皮筋的长为 $d$,求 $d$ 的取值范围.
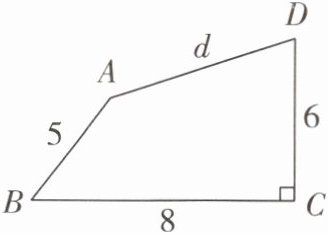

答案:
解:如图1,连接BD。
∵∠C=90°,BC=8,CD=6,
∴BD=√(BC²+CD²)=√(8²+6²)=10。
∵AB可以绕点B任意旋转,
∴分情况讨论如下:

 ①如图2,当点A在线段BD上时,d=10 - 5=5。②如图3,当点A在线段DB的延长线上时,d=5+10=15。综上,5≤d≤15。
①如图2,当点A在线段BD上时,d=10 - 5=5。②如图3,当点A在线段DB的延长线上时,d=5+10=15。综上,5≤d≤15。
解:如图1,连接BD。
∵∠C=90°,BC=8,CD=6,
∴BD=√(BC²+CD²)=√(8²+6²)=10。
∵AB可以绕点B任意旋转,
∴分情况讨论如下:


 ①如图2,当点A在线段BD上时,d=10 - 5=5。②如图3,当点A在线段DB的延长线上时,d=5+10=15。综上,5≤d≤15。
①如图2,当点A在线段BD上时,d=10 - 5=5。②如图3,当点A在线段DB的延长线上时,d=5+10=15。综上,5≤d≤15。 9 新考法 主题:制作无盖正方体形纸盒.
素材:一张正方形纸板.
步骤 1:如图 1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤 2:如图 2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
(1) 直接写出纸板上 $\angle ABC$ 与纸盒上 $\angle A_1B_1C_1$ 的大小关系;
(2) 证明(1)中你发现的结论.
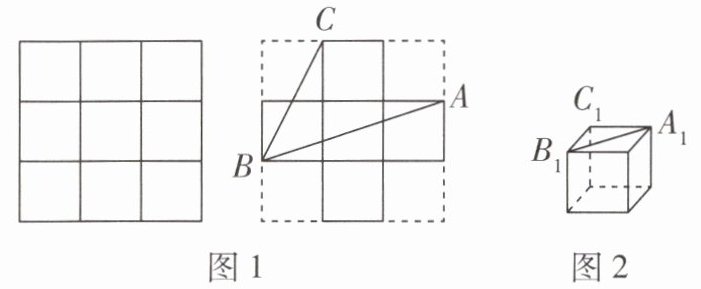
素材:一张正方形纸板.
步骤 1:如图 1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤 2:如图 2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
(1) 直接写出纸板上 $\angle ABC$ 与纸盒上 $\angle A_1B_1C_1$ 的大小关系;
(2) 证明(1)中你发现的结论.

答案:
(1)解:∠ABC=∠A₁B₁C₁。
(2)证明:如图,连接AC,设小正方形的边长为1,则AC=BC=√(1²+2²)=√5,AB=√(1²+3²)=√10。
∵AC²+BC²=5+5=AB²,
∴△ABC为等腰直角三角形。
∵A₁C₁=B₁C₁=√5,A₁C₁⊥B₁C₁,
∴△A₁B₁C₁为等腰直角三角形,
∴∠ABC=∠A₁B₁C₁=45°。
(1)解:∠ABC=∠A₁B₁C₁。
(2)证明:如图,连接AC,设小正方形的边长为1,则AC=BC=√(1²+2²)=√5,AB=√(1²+3²)=√10。
∵AC²+BC²=5+5=AB²,
∴△ABC为等腰直角三角形。
∵A₁C₁=B₁C₁=√5,A₁C₁⊥B₁C₁,
∴△A₁B₁C₁为等腰直角三角形,
∴∠ABC=∠A₁B₁C₁=45°。

10 推理能力 在 $\triangle ABC$ 中,$AB = 15,AC = 20,D$ 是 $BC$ 边所在直线上的点,$AD = 12,BD = 9$,求 $BC$ 的长.
答案:
解:①如图1,当点D在线段BC上时。
∵AD=12,BD=9,AB=15,
∴AD²+BD²=AB²,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴DC=√(AC² - AD²)=√(20² - 12²)=16,
∴BC=BD+CD=9+16=25。 ②如图2,当点D在CB的延长线上时。同理可得DC=16,
②如图2,当点D在CB的延长线上时。同理可得DC=16,
∴BC=CD - BD=16 - 9=7。
∵AC>AB,
∴点D不在BC的延长线上。综上,BC的长度为25或7。
解:①如图1,当点D在线段BC上时。
∵AD=12,BD=9,AB=15,
∴AD²+BD²=AB²,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴DC=√(AC² - AD²)=√(20² - 12²)=16,
∴BC=BD+CD=9+16=25。
 ②如图2,当点D在CB的延长线上时。同理可得DC=16,
②如图2,当点D在CB的延长线上时。同理可得DC=16,∴BC=CD - BD=16 - 9=7。
∵AC>AB,
∴点D不在BC的延长线上。综上,BC的长度为25或7。

查看更多完整答案,请扫码查看


