《2025年一遍过八年级数学上册华师大版》

10 已知$a^{2} + a - 4 = 0$,则代数式$(a^{2} - 5)a$的值是(-4)
A.4
B.-4
C.2
D.-2

答案： B
∵$a^{2}+a - 4 = 0$,
∴$a^{2}+a = 4$,$a^{2}=4 - a$,
∴$(a^{2}-5)a = (-a - 1)a=-a^{2}-a=-(a^{2}+a)=-4$.

11 代数式$3a(a^{2} + ab) - 6a^{3}b + 5a^{2} + 3ab(2a^{2} - a)$的值(B)

A.与$a$,$b$都有关
B.只与$a$有关
C.只与$b$有关
D.与$a$,$b$都无关

答案： B $3a(a^{2}+ab)-6a^{3}b + 5a^{2}+3ab(2a^{2}-a)=3a^{3}+3a^{2}b-6a^{3}b + 5a^{2}+6a^{3}b-3a^{2}b=3a^{3}+5a^{2}$,
∴代数式$3a(a^{2}+ab)-6a^{3}b + 5a^{2}+3ab(2a^{2}-a)$的值只与a有关.

12 某同学在计算一个多项式乘以$2a$时,因抄错运算符号,算成了加上$2a$,得到的结果是$a^{2} + 2a - 1$,那么正确的计算结果是$2a^{3}-2a$.

答案： $2a^{3}-2a$ $[(a^{2}+2a - 1)-2a]\cdot 2a=(a^{2}-1)\cdot 2a = 2a^{3}-2a$.

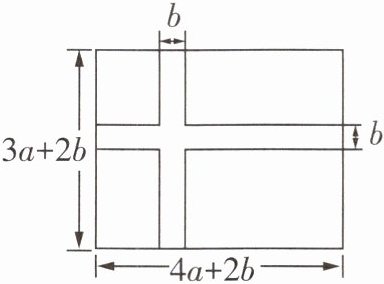
13 [2025 临汾段考]为提升游客游园的舒适度,某公园准备在一个长为$(4a + 2b)$m、宽为$(3a + 2b)$m的长方形草坪上修建两条宽为$b$ m的绿色观光道路(如图),则道路的面积为$7ab + 3b^{2}$m^2.

答案： $7ab + 3b^{2}$ 根据题意,得道路的面积$=b(3a + 2b)+b(4a + 2b)-b^{2}=3ab + 2b^{2}+4ab + 2b^{2}-b^{2}=(7ab + 3b^{2})(m^{2})$.

14 先化简,再求值：$(-3a)^{2} - 2a(-ab + 3b^{2}) + 4(ab^{2} - \frac{1}{2}a^{2}b - \frac{9}{4}a^{2})$,其中$a$,$b满足(a - 4)^{2} + |b + \frac{3}{2}| = 0$.

答案： $(-3a)^{2}-2a(-ab + 3b^{2})+4(ab^{2}-\frac{1}{2}a^{2}b-\frac{9}{4}a^{2})=9a^{2}+2a^{2}b-6ab^{2}+4ab^{2}-2a^{2}b-9a^{2}=-2ab^{2}$.
∵$(a - 4)^{2}+|b+\frac{3}{2}| = 0$,$(a - 4)^{2}\geq 0$,$|b+\frac{3}{2}|\geq 0$,
∴$(a - 4)^{2}=0$,$|b+\frac{3}{2}| = 0$,
∴$a - 4 = 0$,$b+\frac{3}{2}=0$,
∴$a = 4$,$b = -\frac{3}{2}$,
∴原式$=-2×4×(-\frac{3}{2})^{2}=-8×\frac{9}{4}=-18$.

15 把任意数对$(a,b)$放入魔盒后,可得到新运算$(a - 1)(b - 2)$,现在把数对$(m,1)$放入该魔盒,得到结果$n$,则把数对$(n,m)$再次放入该魔盒,得到的结果是多少？

答案： 根据题意,得$n=(m - 1)×(1 - 2)=-m + 1$.把数对(n,m)再次放入该魔盒,得到的结果为$(-m + 1 - 1)(m - 2)=-m(m - 2)=-m^{2}+2m$.

16 对$a$,$b$定义一种新运算：$a * b = a^{2} + ab - b$.如：$(-m) * (-2) = (-m)^{2} + (-m) \cdot (-2) - (-2) = m^{2} + 2m + 2$.求$(-mn) * [mn * (-n)]$的值.

答案： $(-mn)*[mn*(-n)]=(-mn)*[(mn)^{2}+(mn)\cdot (-n)-(-n)]=(-mn)*(m^{2}n^{2}-mn^{2}+n)=(-mn)^{2}+(-mn)(m^{2}n^{2}-mn^{2}+n)-(m^{2}n^{2}-mn^{2}+n)=m^{2}n^{2}-m^{3}n^{3}+m^{2}n^{3}-mn^{2}-m^{2}n^{2}+mn^{2}-n=(m^{2}n^{2}-m^{2}n^{2})-m^{3}n^{3}+m^{2}n^{3}+(mn^{2}-mn^{2})-n=-m^{3}n^{3}+m^{2}n^{3}-n$.

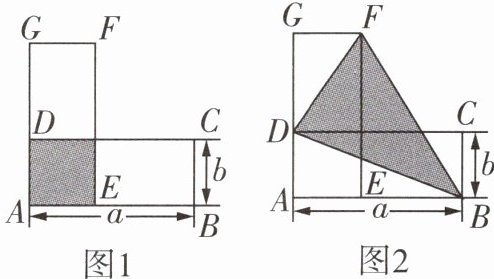
17 [几何直观]如图是两个形状、大小相同的长方形$ABCD和AEFG$,点$E在AB$边上,$AB = a$,$BC = b$,且$a ＞ b ＞ 0$.
(1)图1中阴影部分的面积为______.(用含$a$,$b$的代数式表示)
(2)如图2,连接$BD$,$DF$,$BF$,试比较三角形$ABD与三角形DFG$面积的大小,并说明理由.
(3)求图2中阴影部分的面积.(用含$a$,$b$的代数式表示)

(1)图1中阴影部分的面积为$b^{2}$.(用含$a$,$b$的代数式表示)
(2)$S_{三角形ABD}＞S_{三角形DFG}$;理由如下:$S_{三角形ABD}=\frac{1}{2}ab$,$S_{三角形DFG}=\frac{1}{2}b(a - b)=\frac{1}{2}ab-\frac{1}{2}b^{2}$.
∵$S_{三角形ABD}-S_{三角形DFG}=\frac{1}{2}ab-(\frac{1}{2}ab-\frac{1}{2}b^{2})=\frac{1}{2}ab-\frac{1}{2}ab+\frac{1}{2}b^{2}=\frac{1}{2}b^{2}$,$a＞b＞0$,
∴$\frac{1}{2}b^{2}＞0$,
∴$S_{三角形ABD}＞S_{三角形DFG}$.
(3)求图2中阴影部分的面积.(用含$a$,$b$的代数式表示)
$\frac{1}{2}a^{2}+\frac{1}{2}b^{2}-\frac{1}{2}ab$

答案：
(1)$b^{2}$题图1中阴影部分的面积为$AE\cdot AD=b^{2}$.
(2)$S_{三角形ABD}＞S_{三角形DFG}$;理由如下:$S_{三角形ABD}=\frac{1}{2}ab$,$S_{三角形DFG}=\frac{1}{2}b(a - b)=\frac{1}{2}ab-\frac{1}{2}b^{2}$.
∵$S_{三角形ABD}-S_{三角形DFG}=\frac{1}{2}ab-(\frac{1}{2}ab-\frac{1}{2}b^{2})=\frac{1}{2}ab-\frac{1}{2}ab+\frac{1}{2}b^{2}=\frac{1}{2}b^{2}$,$a＞b＞0$,
∴$\frac{1}{2}b^{2}＞0$,
∴$S_{三角形ABD}＞S_{三角形DFG}$.
(3)如图,延长BC,GF交于点I.$S_{阴影}=S_{正方形ABIG}-S_{三角形ABD}-S_{三角形DFG}-S_{三角形BIF}=a^{2}-\frac{1}{2}ab-\frac{1}{2}(a - b)b-\frac{1}{2}a(a - b)=a^{2}-\frac{1}{2}ab-\frac{1}{2}ab+\frac{1}{2}b^{2}-\frac{1}{2}a^{2}+\frac{1}{2}ab=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}-\frac{1}{2}ab$.