第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8 [2025 唐山期末]下列所作 OP 平分$\angle AOB$的方案,正确的是(

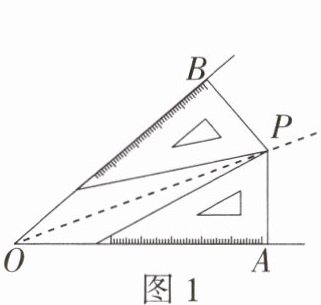
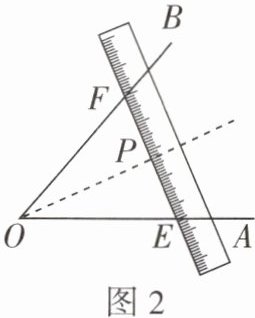
A.只有甲对
B.只有乙对
C.甲、乙都对
D.甲、乙都不对
C
)


A.只有甲对
B.只有乙对
C.甲、乙都对
D.甲、乙都不对
答案:
C 甲的方案中,
∵PB⊥OB,PA⊥OA,BP=AP,
∴OP 平分∠AOB(角的内部到角两边距离相等的点在角的平分线上).乙的方案中,
∵OE=OF,
∴△OEF 是等腰三角形.
∵PE=PF,
∴OP 平分∠AOB(“等腰三角形的三线合一”).
∵PB⊥OB,PA⊥OA,BP=AP,
∴OP 平分∠AOB(角的内部到角两边距离相等的点在角的平分线上).乙的方案中,
∵OE=OF,
∴△OEF 是等腰三角形.
∵PE=PF,
∴OP 平分∠AOB(“等腰三角形的三线合一”).
9 [教材 P107 练习 T1 变式]如图,直线$l_1,l_2,l_3$表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
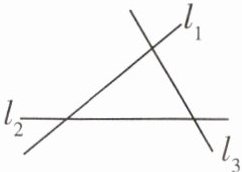
A.一处
B.两处
C.三处
D.四处
D
)
A.一处
B.两处
C.三处
D.四处
答案:
D 因为角的内部到角两边距离相等的点在角的平分线上,所以可供选择的地址可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处.如图,可供选择的地址有 P₁,P₂,P₃,P₄,共四处.
10 如图,$\triangle ABC的周长是60$cm,面积是$600$cm^2,$BP,CP,AP是\triangle ABC$的角平分线,求点 P 到 BC 的距离.
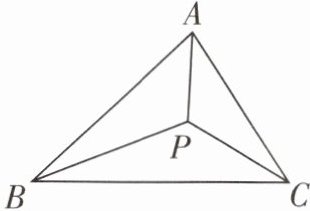

答案:
解:
∵BP,CP,AP是△ABC的角平分线,
∴点 P 到 AB,BC,AC 的距离相等.设点 P 到 AB,BC,AC 的距离为 h.
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴600=1/2AB·h+1/2BC·h+1/2AC·h=1/2h(AB+BC+AC).
∵△ABC 的周长为 60 cm,
∴AB+BC+AC=60 cm,
∴600=1/2h×60,解得 h=20,
∴点 P 到 BC 的距离是 20 cm.
∵BP,CP,AP是△ABC的角平分线,
∴点 P 到 AB,BC,AC 的距离相等.设点 P 到 AB,BC,AC 的距离为 h.
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴600=1/2AB·h+1/2BC·h+1/2AC·h=1/2h(AB+BC+AC).
∵△ABC 的周长为 60 cm,
∴AB+BC+AC=60 cm,
∴600=1/2h×60,解得 h=20,
∴点 P 到 BC 的距离是 20 cm.
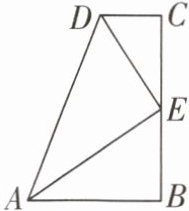
11 [2025 十堰期末]如图,$\angle B = \angle C = 90^{\circ}$,E 是 BC 的中点,DE 平分$\angle ADC$. 求证:(1)AE 是$\angle DAB$的平分线;(2)$AE \perp DE$;(3)$AB + CD = AD$.

答案:
证明:
(1)如图,过点 E 作 EF⊥DA 于点 F.
∵∠C=90°,DE 平分∠ADC,EF⊥DA,
∴CE=EF.
∵E 是 BC 的中点,
∴BE=CE,
∴BE=EF.
∵∠B=90°,EF⊥AD,
∴AE 平分∠BAD,即 AE 是∠DAB 的平分线.
(2)
∵DE 平分∠ADC,AE 平分∠DAB,
∴∠ADE=1/2∠ADC,∠DAE=1/2∠DAB.
∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB//CD,
∴∠ADC+∠DAB=180°,
∴∠ADE+∠DAE=1/2∠ADC+1/2∠DAB=1/2(∠ADC+∠DAB)=90°,
∴∠AED=180°-(∠ADE+∠DAE)=90°,
∴AE⊥DE.
(3)在 Rt△DFE 和 Rt△DCE 中,
∵DE=DE,EF=EC,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC.同理可得,AF=AB.
∵AD=AF+DF,
∴AD=AB+CD,即 AB+CD=AD.
(1)如图,过点 E 作 EF⊥DA 于点 F.
∵∠C=90°,DE 平分∠ADC,EF⊥DA,
∴CE=EF.
∵E 是 BC 的中点,
∴BE=CE,
∴BE=EF.
∵∠B=90°,EF⊥AD,
∴AE 平分∠BAD,即 AE 是∠DAB 的平分线.
(2)
∵DE 平分∠ADC,AE 平分∠DAB,
∴∠ADE=1/2∠ADC,∠DAE=1/2∠DAB.
∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB//CD,
∴∠ADC+∠DAB=180°,
∴∠ADE+∠DAE=1/2∠ADC+1/2∠DAB=1/2(∠ADC+∠DAB)=90°,
∴∠AED=180°-(∠ADE+∠DAE)=90°,
∴AE⊥DE.
(3)在 Rt△DFE 和 Rt△DCE 中,
∵DE=DE,EF=EC,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC.同理可得,AF=AB.
∵AD=AF+DF,
∴AD=AB+CD,即 AB+CD=AD.
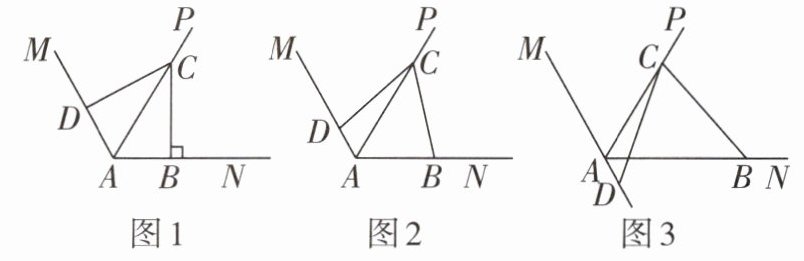
12 [推理能力][2024 保定期末]已知$\angle MAN$,AP 平分$\angle MAN$,定点 C 在射线 AP 上,$\angle DCB$与射线 AN 交于点 B,与直线 AM 交于点 D,且$\angle MAN + \angle DCB = 180^{\circ}$.
【证明】
(1)如图 1,当点 D 在射线 AM 上,且$CB \perp AN$时,AB 的长为 5. 求证:①$CD = CB$;②$AB + AD = 10$.
【探究】
(2)如图 2,当点 D 在射线 AM 上,且 CB 与 AN 不垂直时,(1)中的结论②是否仍然成立? 若成立,请给出证明;若不成立,请说明理由.
【拓展】
(3)如图 3,当点 D 在射线 AM 的反向延长线上时,(1)中的结论②是否仍然成立? 若成立,请直接回答;若不成立,你又能得出什么结论? 请说明理由.
]
【证明】
(1)如图 1,当点 D 在射线 AM 上,且$CB \perp AN$时,AB 的长为 5. 求证:①$CD = CB$;②$AB + AD = 10$.
【探究】
(2)如图 2,当点 D 在射线 AM 上,且 CB 与 AN 不垂直时,(1)中的结论②是否仍然成立? 若成立,请给出证明;若不成立,请说明理由.
【拓展】
(3)如图 3,当点 D 在射线 AM 的反向延长线上时,(1)中的结论②是否仍然成立? 若成立,请直接回答;若不成立,你又能得出什么结论? 请说明理由.
]

答案:
(1)证明:①在四边形 ABCD 中,
∵∠MAN+∠DCB=180°,
∴∠CDA+∠CBA=360°-180°=180°.
∵CB⊥AN,
∴∠CBA=90°,
∴∠CDA=90°.
∵AC 平分∠MAN,
∴CD=CB.
②在 Rt△ADC 和 Rt△ABC 中,AC=AC,CD=CB,
∴Rt△ADC≌Rt△ABC(HL),
∴AD=AB=5,
∴AB+AD=10.
(2)解:
(1)中的结论②仍然成立.证明如下:
如图 1,过点 C 分别作 AM 与 AN 的垂线,垂足分别为 E,F,
∴∠CED=∠CFB=90°.与
(1)同理可得 CE=CF,AF=AE=5.
∵∠MAN+∠ECF=180°,∠MAN+∠DCB=180°,
∴∠ECF=∠DCB,
∴∠ECF-∠DCF=∠DCB-∠DCF,即∠ECD=∠FCB.
在△CED 和△CFB 中,∠CED=∠CFB,CE=CF,∠ECD=∠FCB,
∴△CED≌△CFB(ASA),
∴DE=BF,
∴AB+AD=AF+BF+AD=AF+DE+AD=AF+AE=10.
(3)解:
(1)中的结论②不成立,此时 AB - AD = 10.理由如下:
如图 2,由
(2)知∠CED=∠CFB=90°,CE=CF,AF=AE=5.
∵∠MAN+∠ECF=180°,∠MAN+∠DCB=180°,
∴∠ECF=∠DCB,
∴∠ECF-∠DCF=∠DCB-∠DCF,即∠ECD=∠FCB.
在△CED 和△CFB 中,∠CED=∠CFB,CE=CF,∠ECD=∠FCB,
∴△CED≌△CFB(ASA),
∴DE=BF,
∴AB - AD=AF+BF-(DE - AE)=AF+BF - DE+AE=AF+BF - BF+AE=AF+AE=10.
(1)证明:①在四边形 ABCD 中,
∵∠MAN+∠DCB=180°,
∴∠CDA+∠CBA=360°-180°=180°.
∵CB⊥AN,
∴∠CBA=90°,
∴∠CDA=90°.
∵AC 平分∠MAN,
∴CD=CB.
②在 Rt△ADC 和 Rt△ABC 中,AC=AC,CD=CB,
∴Rt△ADC≌Rt△ABC(HL),
∴AD=AB=5,
∴AB+AD=10.
(2)解:
(1)中的结论②仍然成立.证明如下:
如图 1,过点 C 分别作 AM 与 AN 的垂线,垂足分别为 E,F,
∴∠CED=∠CFB=90°.与
(1)同理可得 CE=CF,AF=AE=5.
∵∠MAN+∠ECF=180°,∠MAN+∠DCB=180°,
∴∠ECF=∠DCB,
∴∠ECF-∠DCF=∠DCB-∠DCF,即∠ECD=∠FCB.
在△CED 和△CFB 中,∠CED=∠CFB,CE=CF,∠ECD=∠FCB,
∴△CED≌△CFB(ASA),
∴DE=BF,
∴AB+AD=AF+BF+AD=AF+DE+AD=AF+AE=10.
(3)解:
(1)中的结论②不成立,此时 AB - AD = 10.理由如下:
如图 2,由
(2)知∠CED=∠CFB=90°,CE=CF,AF=AE=5.
∵∠MAN+∠ECF=180°,∠MAN+∠DCB=180°,
∴∠ECF=∠DCB,
∴∠ECF-∠DCF=∠DCB-∠DCF,即∠ECD=∠FCB.
在△CED 和△CFB 中,∠CED=∠CFB,CE=CF,∠ECD=∠FCB,
∴△CED≌△CFB(ASA),
∴DE=BF,
∴AB - AD=AF+BF-(DE - AE)=AF+BF - DE+AE=AF+BF - BF+AE=AF+AE=10.
查看更多完整答案,请扫码查看


