第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 下列语句中,是定义的是(
A.两点之间线段最短
B.整数和分数统称为有理数
C.三角形的角平分线是一条线段
D.同角的余角相等
B
)A.两点之间线段最短
B.整数和分数统称为有理数
C.三角形的角平分线是一条线段
D.同角的余角相等
答案:
B
2 下列真命题能作为基本事实的是(
A.对顶角相等
B.三角形的内角和是 $180^{\circ}$
C.两点确定一条直线
D.内错角相等,两直线平行
C
)A.对顶角相等
B.三角形的内角和是 $180^{\circ}$
C.两点确定一条直线
D.内错角相等,两直线平行
答案:
C
3 “同角或等角的补角相等”是(
A.定义
B.基本事实
C.定理
D.假命题
C
)A.定义
B.基本事实
C.定理
D.假命题
答案:
C
4 下列说法正确的是(
A.命题是定理,定理是命题
B.命题不一定是定理,定理不一定是命题
C.真命题有可能是定理,假命题不可能是定理
D.定理可能是真命题,也可能是假命题
C
)A.命题是定理,定理是命题
B.命题不一定是定理,定理不一定是命题
C.真命题有可能是定理,假命题不可能是定理
D.定理可能是真命题,也可能是假命题
答案:
C
5 下列能作为证明依据的是(
A.已知条件
B.定义和基本事实
C.定理和推论
D.以上都可以
D
)A.已知条件
B.定义和基本事实
C.定理和推论
D.以上都可以
答案:
D
6 如图,$\because b\perp a$(已知),$\therefore\angle 1 = 90^{\circ}$(垂直的定义).$\because c\perp a$(已知),$\therefore\angle 2 = 90^{\circ}$(垂直的定义),$\therefore\angle 1 = \angle 2$,$\therefore b// c$(同位角相等,两直线平行).已知该证明过程是正确的,则其证明的真命题是(
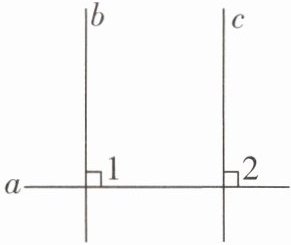
A.在同一平面内,若 $b\perp a$,且 $c\perp a$,则 $b// c$
B.在同一平面内,若 $b// c$,且 $b\perp a$,则 $c\perp a$
C.两直线平行,内错角相等
D.两直线平行,同位角相等
A
)
A.在同一平面内,若 $b\perp a$,且 $c\perp a$,则 $b// c$
B.在同一平面内,若 $b// c$,且 $b\perp a$,则 $c\perp a$
C.两直线平行,内错角相等
D.两直线平行,同位角相等
答案:
A
7 下列推理正确的是(
A.若 $ab > 0$,则 $a + b > 0$
B.若 $a + b > 0$,则 $ab > 0$
C.若 $ab = 0$,则 $a - b = 0$
D.若 $ab = 0$,则 $a = 0$ 或 $b = 0$
D
)A.若 $ab > 0$,则 $a + b > 0$
B.若 $a + b > 0$,则 $ab > 0$
C.若 $ab = 0$,则 $a - b = 0$
D.若 $ab = 0$,则 $a = 0$ 或 $b = 0$
答案:
D A选项,
∵ab>0,
∴a,b同号,
∴a+b>0或a+b<0.B选项,当a=-1,b=2时,a+b>0,但ab<0. C选项,
∵ab=0,
∴a=0或b=0,
∴a-b=0不一定正确. D选项,
∵ab=0,
∴a=0或b=0.
∵ab>0,
∴a,b同号,
∴a+b>0或a+b<0.B选项,当a=-1,b=2时,a+b>0,但ab<0. C选项,
∵ab=0,
∴a=0或b=0,
∴a-b=0不一定正确. D选项,
∵ab=0,
∴a=0或b=0.
8 证明:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.华东师大版教材七上第 183 页的试一试给出了一种方法,请你尝试用其他知识证明.(要求:写出已知,求证,画出图形并给出证明过程)
答案:
解:已知:如图1,直线a//b,b//c.求证:a//c. 证明:如图2,画直线DF分别与直线a,b,c交于点D,E,F.
证明:如图2,画直线DF分别与直线a,b,c交于点D,E,F.
∵a//b(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵b//c(已知),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠3(等量代换),
∴a//c(同位角相等,两直线平行).
解:已知:如图1,直线a//b,b//c.求证:a//c.
 证明:如图2,画直线DF分别与直线a,b,c交于点D,E,F.
证明:如图2,画直线DF分别与直线a,b,c交于点D,E,F.∵a//b(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵b//c(已知),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠3(等量代换),
∴a//c(同位角相等,两直线平行).

9 例 已知 $n > 0$.求证:$m - \dfrac{1}{2}n < m - \dfrac{1}{5}n$.
证明:$\because - \dfrac{1}{2} < - \dfrac{1}{5}$,$n > 0$(已知),
$\therefore - \dfrac{1}{2}n < - \dfrac{1}{5}n$(不等式的基本性质 2),
在不等式的两边都加上 $m$,
得 $m - \dfrac{1}{2}n < m - \dfrac{1}{5}n$(不等式的基本性质 1).
仿照上例,证明下题.
已知 $x < 0$,求证:$2x - 5y > 3x - 5y$.
证明:$\because - \dfrac{1}{2} < - \dfrac{1}{5}$,$n > 0$(已知),
$\therefore - \dfrac{1}{2}n < - \dfrac{1}{5}n$(不等式的基本性质 2),
在不等式的两边都加上 $m$,
得 $m - \dfrac{1}{2}n < m - \dfrac{1}{5}n$(不等式的基本性质 1).
仿照上例,证明下题.
已知 $x < 0$,求证:$2x - 5y > 3x - 5y$.
答案:
证明:
∵2<3,x<0(已知),
∴2x>3x(不等式的基本性质3),在不等式的两边都减去5y,得2x-5y>3x-5y(不等式的基本性质1).
∵2<3,x<0(已知),
∴2x>3x(不等式的基本性质3),在不等式的两边都减去5y,得2x-5y>3x-5y(不等式的基本性质1).
查看更多完整答案,请扫码查看


