《2025年一遍过八年级数学上册华师大版》

11 [2025开封祥符区期末]下列条件中,不能判断△ABC是直角三角形的是 (B)
A.a : b : c = 3 : 4 : 5
B.∠A : ∠B : ∠C = 3 : 4 : 5
C.∠A + ∠B = ∠C
D.a : b : c = 1 : 2 : √{3}

答案： B 选项A,
∵a:b:c=3:4:5,
∴设a=3x,b=4x,c=5x,则(3x)² + (4x)²=(5x)²,
∴△ABC是直角三角形.选项B,
∵∠A:∠B:∠C=3:4:5,
∴设∠A=3x,∠B=4x,∠C=5x,
∴3x + 4x + 5x=180°,解得x=15°,
∴3x=15°×3=45°,4x=15°×4=60°,5x=15°×5=75°,
∴△ABC是锐角三角形.选项C,
∵∠A + ∠B=∠C,∠A + ∠B + ∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.选项D,
∵√3的平方是3,1² + 3=2²,
∴△ABC是直角三角形.解题通法判断一个三角形是不是直角三角形
(1)利用定义从角上判断,即如果已知条件与角度有关,判断是否有一个角度为90°,若有,则是直角三角形,若没有,则不是直角三角形;
(2)利用勾股定理的逆定理从边上判断,即若已知条件与边有关,一般通过计算得出三边的数量关系,看是否符合较短两边的平方和等于最长边的平方,若相等,则是直角三角形,若不相等,则不是直角三角形.

12 [2025安阳期中]已知三角形的三边长分别为a,b,c,且$(a - b)^2 + (a^2 + b^2 - c^2)^2 = 0,$则该三角形的形状是等腰直角三角形。

答案： 等腰直角三角形
∵(a - b)² + (a² + b² - c²)²=0,
∴a - b=0且a² + b² - c²=0,
∴a=b且a² + b²=c²,
∴以a,b,c为边长的三角形是等腰直角三角形.

13 [教材P141复习题T11变式][2025乐山期末]如图,在四边形ABCD中,AB = AD = 6,∠A = 60°,BC = 10,CD = 8,求∠ADC的度数.

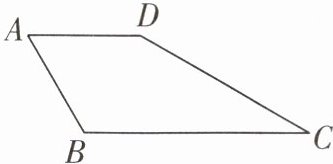
答案：
解:如图,连接BD.
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴BD=6,∠ADB=60°.又
∵CD=8,
∴BD² + CD²=6² + 8²=100.
∵BC²=10²=100,
∴BD² + CD²=BC²,
∴△BDC是直角三角形,且∠BDC=90°,
∴∠ADC=∠ADB + ∠BDC=60° + 90°=150°.

14 [易错题]在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,若$a^2 + b^2 ≠ c^2,$则这个三角形一定不是直角三角形吗？请说明理由.

答案： 解:不一定.理由如下:①当c是最长边时,
∵a² + b²≠c²,
∴△ABC不是直角三角形;②当c不是最长边时,若a² + c²=b²或b² + c²=a²,则△ABC是直角三角形.易错分析本题容易由a² + b²≠c²直接认为△ABC不是直角三角形.在判断时,要分清哪条边是最长边,然后才能运用勾股定理,例如a=6,b=10,c=8,虽然a² + b²≠c²,但是a² + c²=b²,因此以a,b,c为边长的三角形是直角三角形.

15 如图,在△ABC中,AC = 5,BC = 12,AB = 13,将△ABC沿AD折叠,使点C落在AB上的点E处,求DC的长.

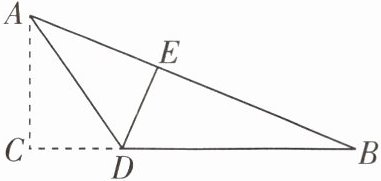
答案： 解:
∵5² + 12²=13²,即AC² + BC²=AB²,
∴△ABC是直角三角形,∠C=90°.根据题意,得AE=AC=5,DC=DE,∠AED=∠BED=∠C=90°.设DC=x,则DE=x,BD=12 - x.在Rt△BDE中,由勾股定理,得x² + (13 - 5)²=(12 - x)²,解得x=10/3,
∴DC=10/3.

16 如图,在△ABC中,AC = 4,BC = 3,AB = 5,AD为△ABC的角平分线,求△ABD的面积.

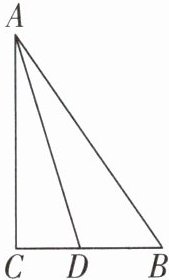
答案：
解:如图,过点D作DE⊥AB于点E.
∵AC=4,BC=3,AB=5,
∴AC² + BC²=AB²,
∴△ABC是直角三角形,且∠C=90°.
∵AD是△ABC的角平分线,DE⊥AB于点E,
∴CD=DE(角平分线的性质).在Rt△ACD和Rt△AED中,
∵AD=AD,CD=ED,
∴Rt△ACD≌Rt△AED(HL).
∴AE=AC=4,
∴BE=AB - AE=5 - 4=1.设BD=x,则DE=CD=BC - BD=3 - x.在Rt△BDE中,BE² + DE²=BD²,
∴1² + (3 - x)²=x²,解得x=5/3.
∴S△ABD=1/2BD·AC=1/2×5/3×4=10/3.

17 [应用意识][2025重庆江北区期末]如图,在河流的一侧有一个村庄C,河边有两个取水点A,B,村庄修建了道路CA和CB,其中CA = AB. 由于某种原因,道路CA不再通行,村庄为了方便村民取水,决定在河边新建一个取水点H(点A,H,B在同一条直线上),并修建道路CH. 经测量,CB = 2.5 km,CH = 2.4 km,HB = 0.7 km.
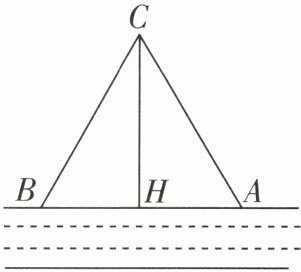
(1)从村庄C到河边的最近道路是CH吗？并说明理由.
(2)道路CH比道路CA近了多少？(结果精确到0.1 km)

答案：
(1) 是。
理由：在$\triangle CHB$中，$CH = 2.4\ km$，$HB = 0.7\ km$，$CB = 2.5\ km$。
根据勾股定理的逆定理，若$CH^{2} + HB^{2} = CB^{2}$，则$\angle CHB = 90{°}$。
计算得$CH^{2} + HB^{2} = 2.4^{2} + 0.7^{2} = 6.25$，$CB^{2} = 2.5^{2} = 6.25$。
因为$CH^{2} + HB^{2} = CB^{2}$，所以$\angle CHB = 90{°}$，即$CH\bot AB$。
根据垂线段最短的性质，从村庄$C$到河边的最近道路是$CH$。
(2) 设$CA = x\ km$，则$AB = x\ km$，$AH = (x - 0.7)\ km$。
在$Rt\triangle CAH$中，根据勾股定理，$CA^{2} = CH^{2} + AH^{2}$。
即$x^{2} = 2.4^{2} + (x - 0.7)^{2}$。
展开并整理得$x^{2} = 5.76 + x^{2} - 1.4x + 0.49$。
进一步整理得$1.4x = 6.25$，解得$x\approx 4.5$。
所以$CA - CH = 4.5 - 2.4 = 2.1\approx 2.1(km)$。
答：道路$CH$比道路$CA$近了$2.1km$。