《2025年一遍过八年级数学上册华师大版》

1 下列计算错误的是(D)

A.$(x + 1)(x + 4) = x^{2} + 5x + 4$
B.$(a + 4)(a - 5) = a^{2} - a - 20$
C.$(m - 3)(m + 3) = m^{2} - 9$
D.$(y - 3)(y - 6) = y^{2} + 18$

答案： D 易知A,B,C项正确;D项,$(y-3)(y-6)=y^{2}-6y-3y+18=y^{2}-9y+18$,D项错误.

2 [2025 临沂段考]观察下列两个多项式相乘的运算过程.

根据你发现的规律,若$(x + a)\cdot(x + b) = x^{2} - 7x + 12$,则(A)
A.$a = - 3$,$b = - 4$
B.$a = 3$,$b = 4$
C.$a = - 3$,$b = 4$
D.$a = 3$,$b = - 4$

答案： A 根据题意,得$a+b=-7$,$ab=12$.结合选项,得a,b的值可能分别是-3,-4.

3 [2025 周口段考]如图是$A$,$B$,$C$三种卡片,现在需要用它们拼成一个长为$(3a + 2b)$、宽为$(a + b)$的长方形,则需要$A$种卡片、$B种卡片和C$种卡片的张数分别是(D)


A.$3$,$5$,$2$
B.$2$,$3$,$5$
C.$2$,$5$,$3$
D.$3$,$2$,$5$

答案： D
∵该长方形的长为$(3a+2b)$、宽为$(a+b)$,
∴该长方形的面积为$(3a+2b)(a+b)=3a^{2}+2b^{2}+5ab$,
∴需要A种卡片、B种卡片和C种卡片的张数分别是3,2,5.

4 [2025 营口站前区期中]已知关于$x的代数式(x + 2m)(x^{2} - x + \frac{1}{2}n)中不含x项与x^{2}$项.
(1)求$m$,$n$的值;
(2)求代数式$m^{2025}n^{2024}$的值.

答案： 解:
(1)$(x+2m)(x^{2}-x+\frac {1}{2}n)$
$=x^{3}-x^{2}+\frac {1}{2}nx+2mx^{2}-2mx+mn$
$=x^{3}+(2m-1)x^{2}+(\frac {1}{2}n-2m)x+mn.$
∵该代数式中不含x项与$x^{2}$项,
$\therefore \left\{\begin{array}{l} 2m-1=0,\\ \frac {1}{2}n-2m=0,\end{array}\right. $解得$\left\{\begin{array}{l} m=\frac {1}{2},\\ n=2.\end{array}\right. $
(2)$m^{2025}n^{2024}=(\frac {1}{2})^{2025}×2^{2024}=(\frac {1}{2}×2)^{2024}×\frac {1}{2}=\frac {1}{2}.$

5 [2025 眉山期末]如图,在一块长为$4$m、宽为$3$m 的长方形空地上,规划一块长方形花园(图中阴影部分),花园的三面留有宽度为$x$m($0 ＜ x ＜ 1$)的小路(图中空白部分),则花园的面积为(D)


A.$(2x^{2} - 10x + 6)$m$^{2}$
B.$(4x^{2} - 10x + 12)$m$^{2}$
C.$(4x^{2} + 10x - 12)$m$^{2}$
D.$(2x^{2} - 10x + 12)$m$^{2}$

答案： D 根据题意,得花园的长为$(4-2x)m$、宽为$(3-x)m$,
∴花园的面积为$(4-2x)(3-x)=(2x^{2}-10x+12)(m^{2}).$

6 [2025 濮阳期末]小明计划用一个长为$(a + 2b)$cm、宽为$(a + b)$cm 的长方形纸板(如图 1)做一个无盖的长方体纸盒,他裁切的方法是先把该长方形的四个角各截去一个边长为$\frac{1}{2}b$cm 的小正方形(如图 2 中的阴影部分),再沿虚线折起来,便做成一个无盖的长方体纸盒.
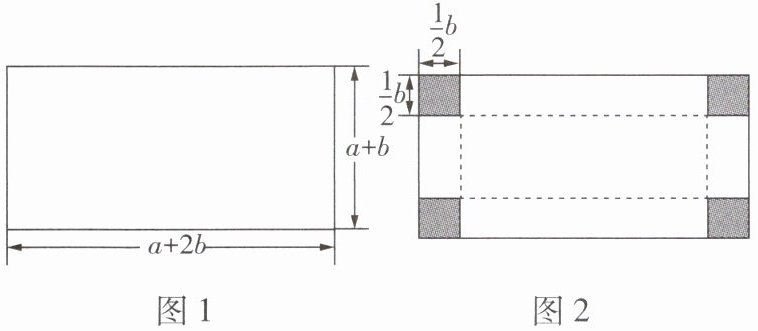
(1)若将该长方体纸盒的外表面都贴上彩纸,则小明至少需要准备的彩纸的面积是多少?(用含$a$,$b$的代数式表示)
(2)当$a = 8$cm,$b = 6$cm 时,求所需彩纸的面积.

答案： 解:
(1)根据题意得,
小明至少需要准备的彩纸的面积是$(a+2b)(a+b)-4×\frac {1}{2}b\cdot \frac {1}{2}b=a^{2}+ab+2ab+2b^{2}-b^{2}=(a^{2}+b^{2}+3ab)(cm^{2}).$
(2)当$a=8cm$,$b=6cm$时,
$a^{2}+b^{2}+3ab=64+36+144=244(cm^{2}),$
∴所需彩纸的面积为$244cm^{2}.$