《2025年一遍过八年级数学上册华师大版》

1 [2024 德州中考]在 $ 0,\frac{1}{2},-2,\sqrt{2} $ 这四个数中,最小的数是(C)
A.$ 0 $
B.$ \frac{1},{2} $
C.$ -2 $
D.$ \sqrt{2} $

答案： C

2 下列实数中,比 $ -3 $ 小的数是(D)
A.$ -1 $
B.$ -2 $
C.$ 0 $
D.$ -5 $

答案： D

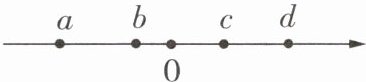
3 [2024 深圳中考]如图,实数 $ a,b,c,d $ 在数轴上表示如下,则最小的实数为(A)

A.$ a $
B.$ b $
C.$ c $
D.$ d $

答案： A

4 [2025 杭州期中]将 $ -3,\sqrt{\frac{1},{4}},(-2)^2,-(-1),\sqrt[3]{27} $ 在如图所示的数轴上表示出来,并用“$ ＜ $”号连接.

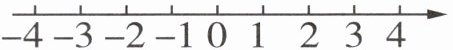
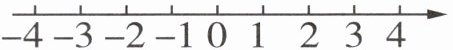
答案：
解:$\sqrt{\frac{1}{4}}=\frac{1}{2}$,$(-2)^2=4$,$-(-1)=1$,$\sqrt[3]{27}=3$,
在数轴上表示如下:
　　　　　
由数轴可知,$-3＜\sqrt{\frac{1}{4}}＜-(-1)＜\sqrt[3]{27}＜(-2)^2$.

5 [2024 山西中考]比较大小：$ \sqrt{6} $＞$ 2 $.(填“$ ＞ $”“$ ＜ $”或“$ = $”)

答案： ＞ $\because (\sqrt{6})^2=6$,$2^2=4$,$6＞4$,$\therefore \sqrt{6}＞2$.

6 比较下列各对数的大小：
(1) $ \sqrt[3]{-26} $ 与 $ -3 $；
(2) $ -\sqrt{50} $ 与 $ -7\frac{1},{2} $.

答案： 解:
(1)$\because (\sqrt[3]{-26})^3=-26$,$(-3)^3=-27$,
$-26＞-27$,$\therefore \sqrt[3]{-26}＞-3$.
(2)$\because (-\sqrt{50})^2=50$,$(-7\frac{1}{2})^2=(-\frac{15}{2})^2=\frac{225}{4}$,
$50＜\frac{225}{4}$,$\therefore -\sqrt{50}＞-7\frac{1}{2}$.

7 比较下列各对数的大小：
(1) $ \sqrt{6} $ 与 $ 2.7 $；
(2) $ \sqrt{5}+2 $ 与 $ 4.3 $.

答案： 解:
(1)利用计算器计算可得,$\sqrt{6}\approx2.45$.
$\because 2.45＜2.7$,$\therefore \sqrt{6}＜2.7$.
(2)利用计算器计算可得,$\sqrt{5}\approx2.24$,$\therefore \sqrt{5}+2\approx4.24$.
$\because 4.24＜4.3$,$\therefore \sqrt{5}+2＜4.3$.

8 课堂上,老师出了一道题：比较 $ \frac{\sqrt{19}-2},{3} $ 与 $ \frac{2},{3} $ 的大小. 小明的解法如下：
解：$ \frac{\sqrt{19}-2},{3}-\frac{2},{3}= \frac{\sqrt{19}-2 - 2},{3}= \frac{\sqrt{19}-4},{3} $.
$ \because 4^2 = 16 ＜ 19,\therefore \sqrt{19} ＞ 4,\therefore \sqrt{19} - 4 ＞ 0 $,
$ \therefore \frac{\sqrt{19}-4},{3} ＞ 0,\therefore \frac{\sqrt{19}-2},{3} ＞ \frac{2},{3} $.
我们把这种比较大小的方法称为作差法.
利用上述方法比较 $ \frac{9-\sqrt{22}},{4} $ 与 $ \frac{3},{4} $ 的大小.

答案： 解:$\frac{9-\sqrt{22}}{4}-\frac{3}{4}=\frac{9-\sqrt{22}-3}{4}=\frac{6-\sqrt{22}}{4}$.
$\because 6^2=36＞22$,$\therefore 6＞\sqrt{22}$,$\therefore 6-\sqrt{22}＞0$,
$\therefore \frac{6-\sqrt{22}}{4}＞0$,$\therefore \frac{9-\sqrt{22}}{4}＞\frac{3}{4}$.

9 [2024 广安中考] $ 3 - \sqrt{9} = $0.

答案： 0 $3-\sqrt{9}=3-3=0$.

10 [2024 包头中考]计算：$ \sqrt[3]{8}+(-1)^{2024} = $3.

答案： 3 $\sqrt[3]{8}+(-1)^{2024}=2+1=3$.

11 计算：
(1) $ \sqrt{49}+\sqrt[3]{-8}+\sqrt{(-5)^2} $；
(2) $ -1^4 + |\sqrt{3} - 2| + \sqrt{3} $.

答案： 解:
(1)$\sqrt{49}+\sqrt[3]{-8}+\sqrt{(-5)^2}=7-2+5=10$.
(2)$-1^4+|\sqrt{3}-2|+\sqrt{3}=-1+2-\sqrt{3}+\sqrt{3}=1$.