第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
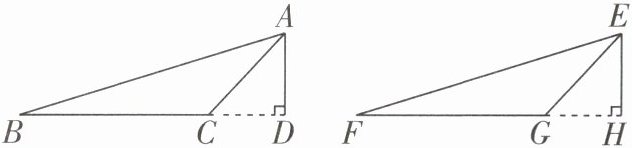
6 如图1,已知$Rt\triangle ABC$,作一个$Rt\triangle A'B'C'$,使得$Rt\triangle A'B'C'\congRt\triangle ABC$.在已有$\angle MB'N = 90^{\circ}$的条件下,图2、图3分别是甲、乙两同学的作图过程.下列说法错误的是(
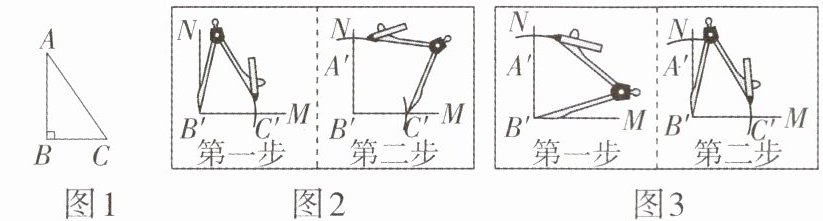
A.甲同学作图判定$Rt\triangle A'B'C'\congRt\triangle ABC$的依据是“$HL$”
B.甲同学第二步作图时,用圆规截取的长度是线段$AC$的长
C.乙同学作图判定$Rt\triangle A'B'C'\congRt\triangle ABC$的依据是“$SAS$”
D.乙同学第一步作图时,用圆规截取的长度是线段$AC$的长
D
)
A.甲同学作图判定$Rt\triangle A'B'C'\congRt\triangle ABC$的依据是“$HL$”
B.甲同学第二步作图时,用圆规截取的长度是线段$AC$的长
C.乙同学作图判定$Rt\triangle A'B'C'\congRt\triangle ABC$的依据是“$SAS$”
D.乙同学第一步作图时,用圆规截取的长度是线段$AC$的长
答案:
D 甲同学第一步作图时,用圆规截取的长度是线段BC的长,第二步作图时,用圆规截取的长度是线段AC的长,则判定Rt△A'B'C'≌Rt△ABC的依据是“HL”,故选项A,B的说法正确,不符合题意;乙同学第一步作图时,用圆规截取的长度是线段AB的长,第二步作图时,用圆规截取的长度是线段BC的长,则判定Rt△A'B'C'≌Rt△ABC的依据是“SAS”,故选项C的说法正确,选项D的说法错误,选项D符合题意。
7 如图,$D为BC$上一点,过点$D分别作DE\perp AB$,$DF\perp AC$,垂足分别为点$E$,$F$,且$DE = DF$,连接$EF与AD相交于点O$,则下列结论不一定成立的是(
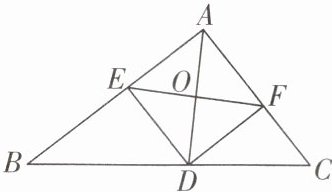
A.$OE = OF$
B.$AE = AF$
C.$OD = OF$
D.$\angle EAD= \angle FAD$
C
)
A.$OE = OF$
B.$AE = AF$
C.$OD = OF$
D.$\angle EAD= \angle FAD$
答案:
C
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.在Rt△ADE和Rt△ADF中,AD=AD,DE=DF,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠EAD=∠FAD.在△AEO和△AFO中,AE=AF,∠EAO=∠FAO,AO=AO,
∴△AEO≌△AFO(SAS),
∴OE=OF.根据题目中的条件,无法判断选项C中的结论是否成立。
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.在Rt△ADE和Rt△ADF中,AD=AD,DE=DF,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠EAD=∠FAD.在△AEO和△AFO中,AE=AF,∠EAO=∠FAO,AO=AO,
∴△AEO≌△AFO(SAS),
∴OE=OF.根据题目中的条件,无法判断选项C中的结论是否成立。
8 [2025潮州期中]如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 12$,$BC = 6$,点$P$,$Q分别在AC和过点A且垂直于AC的射线AX$上运动,$PQ = AB$,当$\triangle PAQ与\triangle ABC$全等时,求$AP$的长.
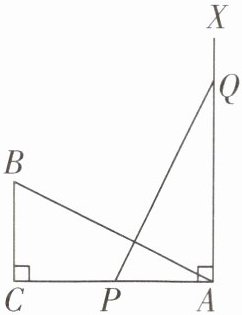

答案:
解:
∵∠C=90°,AX⊥AC,
∴∠C=∠QAP=90°.①当AP=6=BC时,在Rt△ACB和Rt△QAP中,AB=QP,BC=PA,
∴Rt△ACB≌Rt△QAP(HL).②当AP=12=AC时,在Rt△ACB和Rt△PAQ中,AB=PQ,AC=PA,
∴Rt△ACB≌Rt△PAQ(HL).综上,当△PAQ与△ABC全等时,AP的长为6或12。
∵∠C=90°,AX⊥AC,
∴∠C=∠QAP=90°.①当AP=6=BC时,在Rt△ACB和Rt△QAP中,AB=QP,BC=PA,
∴Rt△ACB≌Rt△QAP(HL).②当AP=12=AC时,在Rt△ACB和Rt△PAQ中,AB=PQ,AC=PA,
∴Rt△ACB≌Rt△PAQ(HL).综上,当△PAQ与△ABC全等时,AP的长为6或12。
9 小刚准备证明这样一道题:若两个锐角三角形有两条边和其中一边上的高分别对应相等,则这两个三角形全等.他已经画出图形,并写出了已知和证明(如方框所示).
已知:如图,在$\triangle ABC和\triangle EFG$中,$AC = EG$,$BC = FG$,$AD$,$EH分别是边BC$,$FG$上的高,且$AD = EH$.求证:$\triangle ABC\cong\triangle EFG$.
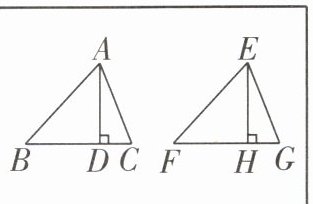
证明:$\because AD和EH分别是\triangle ABC和\triangle EFG的边BC和FG$上的高,$\therefore\angle ADC= \angle EHG = 90^{\circ}$.
在$Rt\triangle ADC和Rt\triangle EHG$中,$AC = EG$,$AD = EH$,
$\thereforeRt\triangle ADC\congRt\triangle EHG(HL)$,$\therefore\angle C= \angle G$.
在$\triangle ABC和\triangle EFG$中,
$BC = FG$,$\angle C= \angle G$,$AC = EG$,$\therefore\triangle ABC\cong\triangle EFG(SAS)$.
(1)如图,若将题目中的条件“两个锐角三角形”改成“两个钝角三角形”,其余条件不变,请你帮他证明该结论仍然成立;
(2)若将题目中的条件“两个锐角三角形”改成“两个三角形”,则该结论______.(填“成立”或“不成立”)
已知:如图,在$\triangle ABC和\triangle EFG$中,$AC = EG$,$BC = FG$,$AD$,$EH分别是边BC$,$FG$上的高,且$AD = EH$.求证:$\triangle ABC\cong\triangle EFG$.
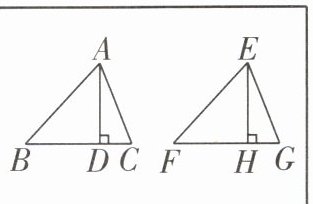
证明:$\because AD和EH分别是\triangle ABC和\triangle EFG的边BC和FG$上的高,$\therefore\angle ADC= \angle EHG = 90^{\circ}$.
在$Rt\triangle ADC和Rt\triangle EHG$中,$AC = EG$,$AD = EH$,
$\thereforeRt\triangle ADC\congRt\triangle EHG(HL)$,$\therefore\angle C= \angle G$.
在$\triangle ABC和\triangle EFG$中,
$BC = FG$,$\angle C= \angle G$,$AC = EG$,$\therefore\triangle ABC\cong\triangle EFG(SAS)$.
(1)如图,若将题目中的条件“两个锐角三角形”改成“两个钝角三角形”,其余条件不变,请你帮他证明该结论仍然成立;
(2)若将题目中的条件“两个锐角三角形”改成“两个三角形”,则该结论______.(填“成立”或“不成立”)

答案:
(1)证明:
∵AD和EH分别是△ABC和△EFG的边BC和FG上的高,
∴∠ADC=∠EHG=90°.在Rt△ADC和Rt△EHG中,AC=EG,AD=EH,
∴Rt△ADC≌Rt△EHG(HL),
∴∠ACD=∠EGH,
∴∠ACB=∠EGF.在△ABC和△EFG中,BC=FG,∠ACB=∠EGF,AC=EG,
∴△ABC≌△EFG(SAS).
(2)解:不成立如图,若一个锐角三角形ABC和一个钝角三角形EFG有两条边(BC=FG,AC=EG)和其中一边上的高(AD=EH)分别对应相等,则这两个三角形不全等.

归纳总结
(1)当两个三角形都是锐角(或钝角)三角形时,若有两条边和其中一边上的高分别对应相等,则这两个三角形全等;
(2)当两个三角形不都是锐角(或钝角)三角形时,若有两条边和其中一边上的高分别对应相等,则这两个三角形不全等。
(1)证明:
∵AD和EH分别是△ABC和△EFG的边BC和FG上的高,
∴∠ADC=∠EHG=90°.在Rt△ADC和Rt△EHG中,AC=EG,AD=EH,
∴Rt△ADC≌Rt△EHG(HL),
∴∠ACD=∠EGH,
∴∠ACB=∠EGF.在△ABC和△EFG中,BC=FG,∠ACB=∠EGF,AC=EG,
∴△ABC≌△EFG(SAS).
(2)解:不成立如图,若一个锐角三角形ABC和一个钝角三角形EFG有两条边(BC=FG,AC=EG)和其中一边上的高(AD=EH)分别对应相等,则这两个三角形不全等.

归纳总结
(1)当两个三角形都是锐角(或钝角)三角形时,若有两条边和其中一边上的高分别对应相等,则这两个三角形全等;
(2)当两个三角形不都是锐角(或钝角)三角形时,若有两条边和其中一边上的高分别对应相等,则这两个三角形不全等。
[回顾与思考]怎样判定两个三角形全等?全等三角形有哪些性质和应用?利用尺规,你能用几种方法作一个三角形与已知三角形全等?
一题练透
全等三角形的性质与判定的应用
如图,线段$BE$,$CD相交于点M$,$BD与CE的延长线相交于点A$.
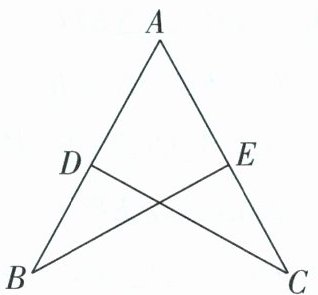
[问题1]若$AB = AC$,$CM = MB$,$\angle C = 30^{\circ}$,求$\angle B$的度数.
[问题2]若$AB = AC$,$AD = AE$,$\angle A = 60^{\circ}$,$\angle C = 25^{\circ}$,求$\angle BMD$的度数.
[问题3]已知$AB = AC$,$\angle B= \angle C$.求证:$BD = CE$.
[问题4]新趋势·过程性学习[教材P116复习题T14变式]如图,连接$AM$,若$\angle ADC= \angle AEB = 90^{\circ}$,$MB = MC$.求证:$\angle1= \angle2$.
小虎同学的证明过程如下.
证明:$\because\angle ADC= \angle AEB = 90^{\circ}$,
$\therefore\angle DMB+\angle B= \angle EMC+\angle C = 90^{\circ}$. …… 第一步
$\because\angle DMB= \angle EMC$,$\therefore\angle B= \angle C$. ………… 第二步
在$\triangle ABM和\triangle ACM$中,
$MA = MA$,$MB = MC$,$\angle B= \angle C$,
$\therefore\triangle ABM\cong\triangle ACM(SSA)$, ………………… 第三步
$\therefore\angle1= \angle2$. ……………………………………… 第四步
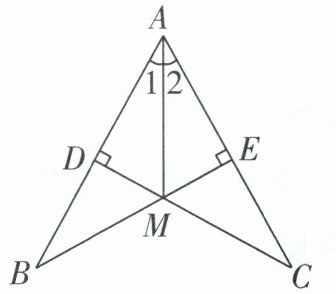
①小虎同学的证明过程中,第____步出现错误;
②请写出正确的证明过程.
一题练透
全等三角形的性质与判定的应用
如图,线段$BE$,$CD相交于点M$,$BD与CE的延长线相交于点A$.

[问题1]若$AB = AC$,$CM = MB$,$\angle C = 30^{\circ}$,求$\angle B$的度数.
[问题2]若$AB = AC$,$AD = AE$,$\angle A = 60^{\circ}$,$\angle C = 25^{\circ}$,求$\angle BMD$的度数.
[问题3]已知$AB = AC$,$\angle B= \angle C$.求证:$BD = CE$.
[问题4]新趋势·过程性学习[教材P116复习题T14变式]如图,连接$AM$,若$\angle ADC= \angle AEB = 90^{\circ}$,$MB = MC$.求证:$\angle1= \angle2$.
小虎同学的证明过程如下.
证明:$\because\angle ADC= \angle AEB = 90^{\circ}$,
$\therefore\angle DMB+\angle B= \angle EMC+\angle C = 90^{\circ}$. …… 第一步
$\because\angle DMB= \angle EMC$,$\therefore\angle B= \angle C$. ………… 第二步
在$\triangle ABM和\triangle ACM$中,
$MA = MA$,$MB = MC$,$\angle B= \angle C$,
$\therefore\triangle ABM\cong\triangle ACM(SSA)$, ………………… 第三步
$\therefore\angle1= \angle2$. ……………………………………… 第四步

①小虎同学的证明过程中,第____步出现错误;
②请写出正确的证明过程.
答案:
解:连接MA.在△ACM和△ABM中,
∵MC=MB,AC=AB,MA=MA,
∴△ACM≌△ABM(SSS),
∴∠B=∠C=30°。
@@解:在△ADC和△AEB中,
∵AD=AE,∠A=∠A,AC=AB,
∴△ADC≌△AEB(SAS),
∴∠B=∠C=25°.
∵∠BDC=∠A+∠C=85°,
∴∠BMD=180°-∠B-∠BDM=180°-25°-85°=70°。
@@证明:在△ACD和△ABE中,
∵∠A=∠A,AC=AB,∠C=∠B,
∴△ACD≌△ABE(ASA),
∴AD=AE,
∴AB-AD=AC-AE,
∴BD=CE。
@@①解:三(没有“SSA”这种判定方法)②证明:
∵∠ADC=∠AEB=90°,
∴∠BDM=∠CEM=90°.在△DMB和△EMC中,∠BDM=∠CEM,∠DMB=∠EMC,MB=MC,
∴△DMB≌△EMC(AAS),
∴MD=ME.在Rt△ADM和Rt△AEM中,MA=MA,MD=ME,
∴Rt△ADM≌Rt△AEM(HL),
∴∠1=∠2。
∵MC=MB,AC=AB,MA=MA,
∴△ACM≌△ABM(SSS),
∴∠B=∠C=30°。
@@解:在△ADC和△AEB中,
∵AD=AE,∠A=∠A,AC=AB,
∴△ADC≌△AEB(SAS),
∴∠B=∠C=25°.
∵∠BDC=∠A+∠C=85°,
∴∠BMD=180°-∠B-∠BDM=180°-25°-85°=70°。
@@证明:在△ACD和△ABE中,
∵∠A=∠A,AC=AB,∠C=∠B,
∴△ACD≌△ABE(ASA),
∴AD=AE,
∴AB-AD=AC-AE,
∴BD=CE。
@@①解:三(没有“SSA”这种判定方法)②证明:
∵∠ADC=∠AEB=90°,
∴∠BDM=∠CEM=90°.在△DMB和△EMC中,∠BDM=∠CEM,∠DMB=∠EMC,MB=MC,
∴△DMB≌△EMC(AAS),
∴MD=ME.在Rt△ADM和Rt△AEM中,MA=MA,MD=ME,
∴Rt△ADM≌Rt△AEM(HL),
∴∠1=∠2。
查看更多完整答案,请扫码查看


